Impact Assessments on Water and Heat Fluxes of Terrestrial Ecosystem Due to Land Use Change
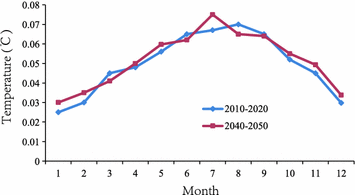
Fig. 5.1
Location map of the study area
Data
Since understanding the interactions between irrigation and changes in the regional heat fluxes and temperature in the future is the main goal of the study, we require high-resolution, spatially explicit data on land use. We used a land use dataset that was derived from the National Aeronautics and Space Administration (NASA) Landsat Thematic Mapper and Enhanced Thematic Mapper (TM/ETM) satellite and analyzed by the Chinese Academy of Sciences (CAS) (Liu et al. 2003a). This national dataset, which has undergone extensive testing and development, contains the most recent information about the extent of different land uses in China for the year 2010. Original land use maps, which have been classified into 6 first-level land use categories and 25 second-level categories, exist at the scale of 1:100,000. The validation test indicates that the average interpretation accuracy for the land use maps is 95 %. The land use maps are further geocoded and stored as 1-km grid data using both the area percentage grid method and the greatest area method. For the greatest area method, if a cell contains more than one polygon and has more than one possible code, the code of the polygon with the greatest area in the cell is used. Land use data operated by the WRF system follow the US Geological Survey’s (USGS) land cover classification scheme. Therefore, we implemented a spatial data mining technique proposed by Wu et al. (2013) to our study area and converted the land use data from the CAS to the USGS classification system. The USGS classification system, which consists of 24 categories, has been widely recognized and used in the simulation studies of climate change. Particularly, we produced the majority of the land cover categories including dryland and irrigated cropland in the USGS system by comparing the relevant subcategories between the CAS and USGS systems using the greatest area grid data. In this way, we generally retained the spatial distribution of land covers in the original high-resolution dataset. The new land cover dataset is a single-layer dataset with ∼1 km spatial resolution, representing 15 land cover categories. Finally, to meet the input requirements of the WRF system, we aggregated the 1-km grid data of the USGS system to the 10-km grid data to facilitate the simulation of atmospheric responses to different land cover scenarios.
We constructed the atmospheric lateral boundary forcing conditions for the period of 2010–2020 using the projected output of future climate change based on the Representative Concentration Pathway 6 (RCP6) from the multimodel dataset of the Coupled Model Intercomparison Project Phase 5 (CMIP5). The RCPs provide four possible climate trajectories, all of which depend on how factors including radiative forcings, technology, economies, lifestyle, and policy will change in the future (Moss et al. 2010). The RCP6, which is developed by the Asia-Pacific Integrated Model (AIM) modeling team at the National Institute for Environmental Studies (NIES), Japan, is a stabilization scenario where total radiative forcing is stabilized after 2100 (Hijioka et al. 2008). The variables that we use to construct the atmospheric forcing conditions from 2010 to 2020 include air temperature, specific humidity, sea-level pressure, u-wind, v-wind, and geopotential height.
Methods
Land Cover Scenarios
Figure 5.2 displays the land cover map of our study area in 2010 represented by the new land cover dataset that is generated from the CAS national land use dataset. This land cover map shows that the contemporary landscape of our study area is characterized by a rich culture of agriculture and the mixture of different land covers. In 2010, the area of cultivated cropland, including dryland and irrigated cropland, takes up 37 % of the total landscape. More than 72 % of the cultivated cropland is irrigated, while the proportion of dryland is relatively small.
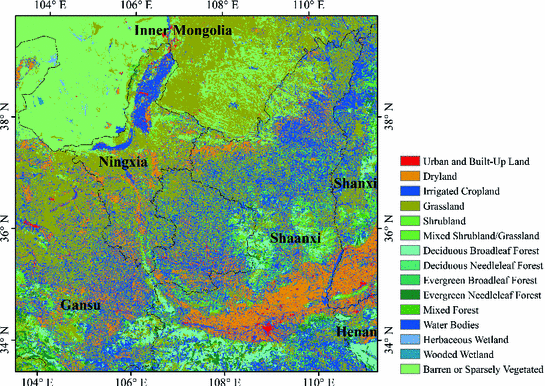
Fig. 5.2
Land cover map of our study area in 2010 represented by the new land cover dataset, with a spatial resolution of 1 km
In order to identify the effects of irrigated agriculture on the energy fluxes and near-surface temperature, we designed three land cover datasets corresponding to three land cover scenarios (Fig. 5.3). The control scenario (CON) assumes that there is no irrigation at all. The irrigation scenario (IRR) assumes that irrigated agriculture maintains at the contemporary scale. The irrigated cropland expansion scenario (ICE) assumes an expansion of the irrigation to all cultivated cropland. For the IRR, we used the new land cover dataset derived from the CAS dataset. For the CON, we selected any grid cell in which the land cover was irrigated cropland in the new land cover dataset and replaced it with the cell of dryland. For the ICE, we selected any grid cell specified as dryland in the new land cover dataset and replaced it with the cell of irrigated cropland. In reality, we expect the potential expansion of irrigated cropland to be limited because we consider that further expansion of irrigation would be largely constrained by the shortage of water resources in northern China. The land cover scenarios defined here are relatively extreme and are intended to help understand the nature and potential magnitude of climate effects of irrigated agriculture. However, based on the modeling results of these scenarios, we can derive useful insights about the actual climate effects of past and future expansion of irrigation over existing cropland.
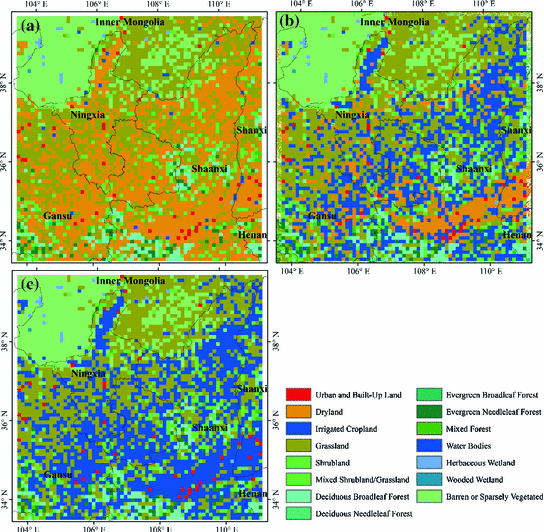
Fig. 5.3
Three land cover scenarios of our study area, with a spatial resolution of ~10 km: a control scenario (CON), b irrigation scenario (IRR), and c irrigated cropland expansion scenario (ICE)
Model Description
We conducted numerical simulations using the WRF modeling system version 2. The WRF model is a fully functioning, next-generation mesoscale forecast model and data assimilation that will advance both the understanding and prediction of mesoscale climate systems and promote the interactions between the atmospheric research and operational communities. It is a three-dimensional, non-hydrostatic, and primitive equation atmospheric modeling system. The WRF model version 2 uses the Eulerian mass coordinate and is referred to as the Advanced Research WRF (ARW) system (Kumar et al. 2008). Compared to the previous versions, changes and updates to the ARW include mixed-phase physics schemes suitable for cloud-resolving modeling, multiple-nesting capabilities that enhance resolution over the areas of interest, and enhanced model coupling Application Program Interface (API) enabling WRF to be coupled with other models such as ocean and land models. The WRF model has been utilized extensively for regional climate, operational numerical weather prediction, and hurricane and storm prediction (Kumar et al. 2008; Mölders 2008). Validation against observational records indicates its high performance in simulating spatial and temporal climatic features.
For all simulation runs, we used a domain centered at 36.7°N, 107°W, with a horizontal resolution of 10 km and with 31 vertical layers. The soil column has four soil layers, with the bottom layer extending to a maximum depth of 3.5 m. In the WRF model, we simulated water vapor and cloud processes using the Single-Moment 3-class (WSM3) scheme (Hong et al. 2004). We used the Grell–Devenyi ensemble cumulus parameterization scheme to account for the subgrid-scale effects of convective and shallow clouds. The surface layer physics followed similarity theory. We parameterized atmospheric boundary layer processes using the Yonsei University (YSU) planetary boundary layer, a non-local K scheme with an explicit treatment of the entrainment layer and parabolic K profile in the unstable mixed layer. We chose the rapid radiative transfer model (RRTM) (Mlawer et al. 1997) as the longwave radiation scheme and MM5 shortwave scheme (Dudhia 1989) as the shortwave radiation scheme. We selected the Smagorinsky scheme for horizontal diffusion and Mellor and Yamada (1982) scheme for vertical diffusion. We used the Noah LSM (Chen and Dudhia 2001) to model land surface processes. The Noah LSM is a four-layer soil temperature and moisture model which calculates thermal and moisture stocks and fluxes at the land–atmosphere interface and may handle vegetation, root, and canopy effects and surface snow-cover prediction.
For irrigated grid cells representing irrigated cropland, our model forces soil moisture at root zone to field capacity at every time step (time step = 30 min), all year round. Field capacity, defined as the maximum amount of water that the unsaturated zone of a soil can hold, is a parameter prescribed based on soil type. Irrigation practices and technologies vary in real cases. However, since most of our study area supports a whole year growing season (Deng et al. 2006a), we use this as a reasonable approximation to actual irrigation. The irrigation water either leaves the surface through evapotranspiration or gets lost as runoff or subsurface drainage. Our model separately simulates three processes of evapotranspiration—ground evaporation, vegetation transpiration, and vegetation evaporation, i.e., evaporation of water intercepted by vegetation canopy. The amount of evapotranspiration is calculated as the sum of the three. For non-irrigated grid cells representing dryland and the other land covers, the LSM determines soil moisture as a function of precipitation, evapotranspiration, infiltration, and soil properties. Initial soil moisture conditions and vegetation parameters specific to different land covers were taken from the parameter files in the Noah LSM. All vegetation interacts with soil moisture from the single vegetated soil column. Like Lobell et al. (2006) and Kueppers et al. (2007), we set atmospheric CO2 concentrations constant at 355 ppm. To study the impacts of land surface changes related to irrigation, we simulated the regional atmospheric dynamics for a period of 11 years (January 1, 2010–December 31, 2020), based on the three land cover scenarios described earlier. We discarded the first year of each simulation as spin-up and compared results from the final 10 years among different scenarios.
Results
Effects of Irrigation on Heat Fluxes
Over the 10-year period of simulations, irrigation displays significant impacts on surface energy budgets, evidenced by the differences in the partitioning of this energy between latent heat and sensible heat for the three land cover scenarios (Fig. 5.4). The conversion from CON to IRR shows an increase in annual mean latent heat fluxes of 12.10 W m−2 and a decrease in annual mean sensible heat fluxes of 8.85 W m−2. The largest increases in annual mean latent heat fluxes occur in the central and eastern parts of Gansu Province. For large areas in the middle and south section of the model domain, where irrigated cropland is densely distributed in IRR, latent heat fluxes increase by 40–80 W m−2. Surface energy budgets appear to change little for areas in the north section of the model domain, where much of the landscape is made up of barren land and grassland. More differences can be identified when irrigation extent expands to all cultivated cropland. The conversion from CON to ICE results in an increase in annual mean latent heat fluxes of 18.08 W m−2 and a decrease in annual mean sensible heat fluxes of 12.31 W m−2. Particularly, the latent heat fluxes increase by 80 W m−2 or more for a broad region in Middle Shaanxi and Shanxi provinces, where large areas of dryland are converted to irrigated cropland. The shift of energy balance away from sensible heat and toward latent heat is primarily due to increased soil moisture associated with irrigated grid cells, which leads to higher rates of evapotranspiration. The annual mean increase in evapotranspiration between the CON and IRR is 0.41 mm/day and is 0.61 mm/day between the CON and ICE.
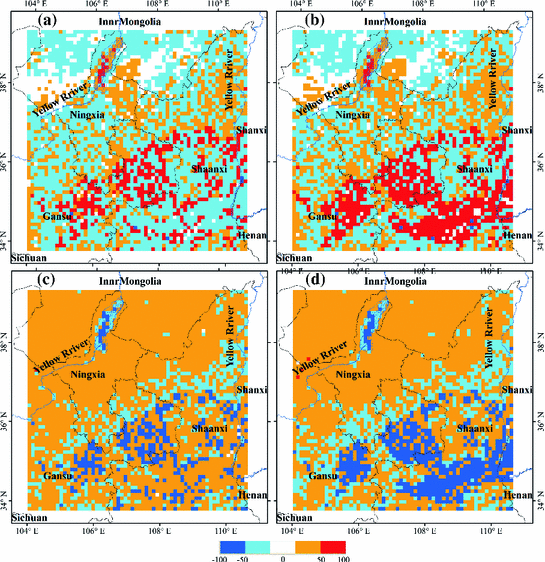
Fig. 5.4
Annually averaged differences in the latent heat fluxes (W m−2) a from CON to IRR and b from CON to ICE. Annually averaged differences in the sensible heat fluxes (W m−2) c from CON to IRR and d from CON to ICE
Interestingly, further expansion of irrigation in ICE not only affects the surface energy budgets of the newly converted land, but also has an impact on the larger surrounding region. For example, many existing irrigated grid cells in IRR experience a further increase in latent heat fluxes in ICE. Our results indicate that the impact of irrigation can move beyond the scope of individual grid cells. This can be partially explained by the processes of irrigation water loss and a likely change in regional precipitation patterns. Despite that a large portion of extra water added from irrigation leaves the surface through evapotranspiration, the rest is lost in the form of runoff and subsurface drainage, both of which may affect hydrology of the areas nearby. Compared to CON, irrigation increases runoff by 37 and 38 mm/year in IRR and ICE, respectively. In addition, previous studies have demonstrated that precipitation feedbacks are not confined at local level (Sacks et al. 2009).
Substantial seasonal variation exists in terms of the magnitude of change in surface energy budgets (Tables 5.1 and 5.2; Fig. 5.5). The increases in latent heat fluxes due to irrigation peak during the summer in both IRR and ICE. From CON to IRR, irrigated land conversion increases latent heat fluxes by 27.79 W m−2 for the summer months (June, July, and August) and by merely 0.50 W m−2 for the winter months (December, January, and February). From CON to ICE, further expansion of irrigated land leads to an increase in latent heat fluxes of 39.41 W m−2 in the summer and only 1.47 W m−2 in the winter. In typical semiarid regions of northern China, as water vapor released into the atmosphere from the water-stressed landscape is limited, surface net radiation is mainly partitioned into sensible heat fluxes. However, irrigation and increased soil moisture can introduce significant latent heat fluxes through surface evaporation and transpiration. Both of these two processes usually peak during the summer, when temperature is relatively high and crop growth peaks. That basically explains why the effect of irrigation on surface energy budgets is much stronger in the summer than in the winter. As expected, there is also significant seasonal difference associated with the change in evapotranspiration and the pattern of this difference agrees with the seasonality of the change in energy fluxes. Similarly, the largest increases of evapotranspiration occur during the summer, with an average increase of 0.95 mm/day for IRR and 1.35 mm/day for ICE, while evapotranspiration increases are small during the winter.
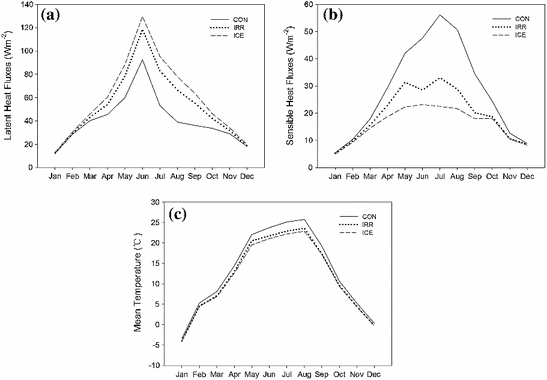
Table 5.1
Domain-averaged differences for climate variables between CON and IRR
T mean (°C) | T max (°C) | T min (°C) | ET (mm/day) | LH (W m−2) | SH (W m−2) | DR (W m−2) | |
|---|---|---|---|---|---|---|---|
Jan | −0.58 | −1.10 | −0.01 | 0.01 | 0.20 | −0.12 | −0.23 |
Feb | −0.75 | −1.27 | −0.09 | 0.03 | 0.85 | −0.57 | −0.78 |
Mar | −1.04 | −1.53 | −0.17 | 0.10 | 2.95 | −2.21 | −1.83 |
Apr | −1.43 | −1.89 | −0.46 | 0.29 | 8.47 | −6.45 | −3.30 |
May | −1.53 | −1.96 | −0.71 | 0.63 | 18.49 | −10.62 | −5.70 |
Jun | −2.02 | −2.56 | −0.98 | 0.89 | 26.06 | −19.07 | −7.46 |
Jul | −2.22 | −2.80 | −1.16 | 1.02 | 29.88 | −23.08 | −8.88 |
Aug | −2.17 | −2.75 | −1.15 | 0.93 | 27.42 | −21.82 | −8.36 |
Sep | −1.92 | −2.47 | −0.85 | 0.65 | 19.16 | −14.28 | −4.99 |
Oct | −1.06 | −1.55 | −0.39 | 0.28 | 8.42 | −5.66 | −3.16 |
Nov | −0.77 | −1.29 | −0.15 | 0.09 | 2.87 | −2.05 | −1.55 |
Dec | −0.59 | −1.12 | −0.03 | 0.01 | 0.45 | −0.23 | −0.36 |
Year | −1.34 | −1.86 | −0.51 | 0.41 | 12.10 | −8.85 | −3.97 |
Table 5.2
Domain-averaged differences for climate variables between CON and ICE
T mean (°C) | T max (°C) | T min (°C) | ET (mm/day) | LH (W m−2) | SH (W m−2) | DR (W m−2) | |
|---|---|---|---|---|---|---|---|
Jan. | −0.57 | −1.24 | −0.09 | 0.03 | 0.91 | −0.45 | −0.40 |
Feb. | −0.79 | −1.48 | −0.13 | 0.06 | 1.98 | −1.03 | −1.12 |
Mar. | −1.23 | −1.88 | −0.23 | 0.19 | 5.77 | −3.32 | −2.80 |
Apr. | −1.82 | −2.42 | −0.55 | 0.51 | 14.90 | −10.63 | −4.44 |
May | −2.54 | −3.30 | −1.06 | 0.97 | 28.49 | −19.71 | −7.67 |
Jun. | −2.67 | −3.42 | −1.23 | 1.27 | 37.09 | −24.46 | −10.03 |
Jul. | −2.96 | −3.77 | −1.45 | 1.44 | 42.23 | −33.61 | −11.94 |
Aug. | −2.88 | −3.68 | −1.44 | 1.32 | 38.91 | −29.02 | −11.25 |
Sep. | −1.97 | −2.58 | −0.88 | 0.93 | 27.49 | −16.43 | −6.71 |
Oct. | −1.32 | −1.97 | −0.45 | 0.42 | 12.59 | −6.31 | −4.25 |
Nov. | −0.88 | −1.54 | −0.16 | 0.16 | 5.03 | −2.12 | −2.14 |
Dec. | −0.61 | −1.26 | −0.10 | 0.05 | 1.52 | −0.59 | −0.50 |
Year | −1.69 | −2.38 | −0.65 | 0.61 | 18.08 | −12.31 | −5.27 |
Fig. 5.5
Annual cycles of a latent heat fluxes; b sensible heat fluxes; and c mean temperature for three land cover scenarios
Effects of Irrigation on Near-Surface Temperature
There are significant changes in near-surface temperature due to irrigation (Fig. 5.6). Converting from CON to IRR, the annual mean temperature of our study area is 1.3 °C lower on average, when a considerable proportion of dryland is converted to irrigated cropland. The irrigation cooling effect is the most significant for areas where irrigated cropland heavily concentrates. Particularly, parts of the middle section of the model domain, including portions of the central and eastern parts of Gansu Province, portions of the southern Ningxia Province, and portions of the central Shaanxi Province, are cooled by 5 °C averaged over the year. Most of the irrigated areas in the north and northeast sections of the model domain are cooled by 3 °C. On the other hand, most desert and grassland areas in the north section of the model domain experience little temperature change. On average, the decrease in annual mean temperature is eight times greater over irrigated areas than over non-irrigated areas. The cooling effect becomes more significant with the further expansion of irrigated land to all cultivated cropland. The conversion from CON to ICE decreases the annual mean temperature of our study area by 1.7 °C. Expansion of irrigated land in the central parts of Shaanxi and Shanxi provinces suppresses the local annual mean temperature by 4–5 °C. Many existing irrigated areas in IRR show a further reduction of annual mean temperature in ICE. Our modeled decreases in near-surface temperature are accompanied by large increases in evapotranspiration and a shift of energy partitioning toward latent heat fluxes. Comparisons between CON and IRR, and between CON and ICE demonstrate that generally areas experiencing significant cooling are consistent with areas that have large increases in latent heat fluxes.
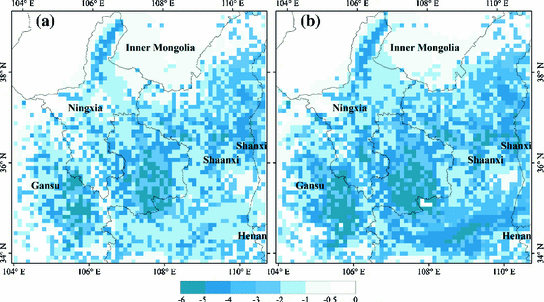
Fig. 5.6
Annually averaged differences in near-surface temperature (°C) a from CON to IRR and b from CON to ICE
There are two mechanisms that could explain the surface cooling effect associated with irrigation. Irrigation increases the latent heat fluxes and decreases the sensible heat fluxes, thereby leading to a direct evaporative cooling of the surface. This is the dominant mechanism that contributes to the cooling effect of irrigation, as suggested by our modeled results about the changes in heat fluxes and near-surface temperature across different land cover scenarios. Furthermore, other factors can strengthen this cooling effect. Increased water vapor in the atmosphere causes an increase in cloud cover, which in turn can result in a greater fraction of reflected solar radiation and a decrease in total downwelling radiation. This non-local mechanism of irrigation is usually called the indirect cooling effect of irrigation (Sacks et al. 2009). Compared to CON, annual mean downwelling radiation of our study area decreases by 3.97 and 5.27 W m−2 in IRR and ICE, respectively. Very likely, this is due to enhanced cloud cover resulting from additional water vapor introduced from irrigation. Clouds can affect the energy distribution in the atmosphere through two mechanisms. Lower-level clouds cool the surface by reflecting solar radiation, while upper-level clouds warm the atmosphere by partially capturing emitted thermal radiation (Stubenrauch et al. 2002). Based on this, it is likely that the increased cloud cover due to irrigation would be lower-level cloud cover. In addition, our modeling results show that the irrigation cooling effect is not restricted to the near-surface atmosphere associated with irrigated areas, but spread to adjacent non-irrigated areas. For example, from CON to ICE, in the central and eastern parts of Gansu Province, and the central Shaanxi Province, even non-irrigated grid cells undergo various degrees of cooling, although the magnitude of this cooling is smaller compared to that of the nearby irrigated grid cells. This indicates that non-local processes such as enhanced cloud cover are probably also important in determining regional surface temperature.
Differences in monthly mean surface temperature for the three land cover scenarios reveal that the impact of irrigation on regional temperature varies substantially across seasons. The cooling effect of irrigation is much stronger in the summer than in the winter. For instance, from CON to ICE, the largest cooling effect occurs in July, with a decrease in mean surface temperature of 3.0 °C, while the smallest cooling effect occurs in January, with a decrease in mean surface temperature of 0.6 °C. This seasonal pattern of the cooling effect is consistent with the seasonality of the changes in evapotranspiration and heat fluxes due to irrigation. This is expected because our results have shown that the dominant cooling effect, the evaporative cooling, reaches its maximum during the summer growing season. In addition, irrigation exerts a stronger cooling effect during the day than night. With the expansion of irrigated cropland in both IRR and ICE, the annual average change in daily maximum temperature is much greater than that in daily minimum temperature, leading to a decrease in the diurnal temperature range. For example, from CON to IRR, the annually averaged maximum temperature decreases by 1.9 °C, while the annually averaged minimum temperature decreases by 0.5 °C. This regional result confirms to the previous finding of Sack et al. (2009) on effects of global irrigation that irrigation mostly affects daytime climate. Since both of the two cooling mechanisms—the evaporative cooling and increased reflected solar radiation due to more cloud cover—tend to peak during the day, the irrigation cooling effect is mainly reflected by a substantial decrease in daily maximum temperature.
Theoretically, lower albedo of irrigated soil may also affect the surface energy balance and regional climate. However, comparing among different scenarios, we find that albedo changes only slightly due to irrigation. For example, the average albedo for areas of cultivated cropland decreases by 0.0073 from CON to IRR, and by 0.001 from IRR to ICE. This magnitude of change in albedo due to irrigation is much smaller relative to that associated with the land conversion between natural vegetation (such as forest and grassland) and cropland. Field measurements have also verified that the differences between irrigated and non-irrigated albedos in our study region are small (Guan et al. 2009). This indicates that in our case, the change in net radiation due to lower albedo of irrigated land accounts for a minimal portion of the change in energy balance and therefore plays a less important role in regional climate. Our finding for this particular region is consistent with the global-scale experimental study of Lobell et al. (2006), which shows that the global temperature changes were highly correlated with changes in net surface radiation, but not with changes in surface albedo.
Our simulated effect of irrigation on the latent heat fluxes in the inland irrigation area of northern China is smaller than estimates in regional studies such as Kuepper et al. (2007), in which irrigation increased the latent heat fluxes in California year-round by 70.7 W m−2, but close in the magnitude to estimates about India in Douglas et al. (2009), southern India in Biggs et al. (2008), and US High Plains in Adegoke et al. (2003). Similarly, although many regional studies have shown significant cooling effects of irrigation, they have disagreed about the magnitude of these effects. Our simulated cooling effect is close in the magnitude to estimates about Nebraska in Mahmood et al. (2006), California in Kueppers et al. (2007), and India in Douglas et al. (2009). Our simulated irrigation cooling in our study region is also consistent with Lee et al. (2011), which found qualitatively similar but smaller temperature decreases over Asia due to irrigation. Differences in the magnitude of the effects of irrigation between these studies can be explained by differences in how irrigation is modeled, the selection and setup of the atmospheric model, the scale of the study region, and other regional heterogeneities.
The design of our WRF model has some limitations. As different crops have distinct irrigation water requirements and timing of irrigation, ideally there could be a crop model that deals with the irrigation status of different crop types. This requires spatially explicit information about crop-type distributions and crop-specific information about agricultural management. Given the data-sparse environment, those data are not available for our study region. Using an average land cover in an irrigation simulation scheme could cause over- or underestimated irrigation water input (Ozdogan et al. 2010). Development of high-resolution land use data about crop types and incorporation of a crop model in the irrigation scheme could be a direction of future work for researchers who intend to explore climatic effects of irrigation.
Summary
Population growth and Westernization of dietary patterns have increased the demand for food, resulting in intensification of agricultural practices in many regions around the world. Expansion of irrigated agriculture has the potential to alter regional to global climate significantly. In this section, we investigate the impacts of irrigation on the heat fluxes and near-surface temperature in the future for a specific region. We focus our study on an inland irrigation area of northern China, an area in the developing world with a long history of irrigated agriculture and high ecological vulnerability. Based on the modeling results of the WRF system, we examine the changes in heat fluxes and near-surface temperature among three land cover scenarios: the CON, the IRR, and the ICE. Our results indicate that the surface energy budgets and temperature are sensitive to changes in the extent and spatial pattern of irrigated land. Conversion to irrigated agriculture at the contemporary scale (as in IRR) leads to an increase in annual mean latent heat fluxes of 12.10 W m−2, a decrease in annual mean sensible heat fluxes of 8.85 W m−2, and a decrease in annual mean temperature of 1.3 °C across the study region. Further expansion of irrigated land to all cultivated cropland (as in ICE) increases annual mean latent heat fluxes by 18.08 W m−2, decreases annual mean sensible heat fluxes by 12.31 W m−2, and decreases annual mean temperature by 1.7 °C. The cooling effects of irrigation tend to be greatest for areas where irrigated cropland heavily concentrates and are much stronger in the summer growing season than in the winter. The seasonality of the cooling effect is consistent with the seasonality of the changes in evapotranspiration and heat fluxes due to irrigation. In addition, we identify that irrigation exhibits a greater cooling effect during the day than night, leading to a decrease in the diurnal temperature range. While direct evaporative cooling plays a dominant role, indirect non-local processes such as enhanced cloud cover are probably also important in causing the cooling of the surface.
Our modeled effects of irrigation show that changes in land use management such as irrigation can be an important component of climate change. Several studies have shown that the regional climate of northern China is becoming warmer and drier and this trend is likely to continue into the future. However, those projections do not account for the climate impacts from land cover and land management change. Regional climate forcings including irrigation expansion can introduce a countervailing cooling effect, weakening the projections of future regional warming from greenhouse gases. Our study has simulated the scenario of expansion of irrigated area, which is likely to take place due to population growth and economic development. In other circumstances, irrigated area may also decline due to lack of sufficient water supply or conversion of irrigated agriculture to urban land. It is expected that these irrigation changes can modify future regional climate and need to be considered together with greenhouse forcing in climate change assessments.
Spatial Variation of Surface Temperature and Precipitation Due to Grassland Conversion to Forestry Area in Southeast China
Introduction
Under the coupled impact of natural processes and human activities over the past century, the global vegetation system has changed correspondingly, which in turn influenced the regional and global climate. The nature of the vegetation affects the surface fluxes of radiation, heat, moisture, and momentum, so modifying the vegetation cover can change the lower boundary conditions of the atmosphere and hence impact the climate (Pielke et al. 1998). Besides, changes in vegetative cover, especially the change of vegetation types, are associated with changes in plants’ morphology and physiology, which could, in the absence of other force, alter the surface fluxes and consequently the climate both at regional and at global scales (Bounoua et al. 2002). In addition, forests and grasses are the most two typical vegetation types on the Earth; however, mankind has significantly changed the Earth surface by transforming natural ecosystems (forests and grasslands) (Brovkin et al. 1999). Furthermore, the conversion of forestland and grassland plays an important role in the climate system, and redistributions of forest and other vegetation (due, e.g., to extensive logging) could initiate important climate feedbacks (Bonan et al. 1992). And a significant difference in surface parameter (such as albedo) between forest and grassland results in reduced absorbed radiation for the grasslands, especially during the snow-thawing season (spring). Also, a forested landscape generally has a lower surface albedo than grassland, particularly in conditions of lying snow when shortwave radiation is trapped by multiple reflections within the forest canopy (Betts and Ball 1997). In fact, the assessment reports of Intergovernmental Panel on Climate Change (IPCC) specifically took agriculture, forestry, and other land use (AFOLU) as a major path to slow the process of global climate change (Landman 2010), and the research on the impact of forestland and grassland transition on climate is of great significance to find the optimal way to mitigate the climate change.
Numerous studies have reported the climate impact of vegetation changes such as deforestation and grassland degradation at different scales. However, little is known about the impact of large-scale conversion from grassland to forestland on climate, especially the scale and degree it may bring about in the future. The deforestation experiments with atmospheric general circulation models (AGCMs) generally agreed in significant cooling in the spring season within the models and argued that different vegetation cover plays the most significant role in determining the climate–vegetation state of the region (Chalita and Le Treut 1994). Further studies carried out in the experiments with the modified Community Climate Model (CCM2) and prescribed sea surface temperature (SST) showed a significant summer cooling effect of grass and forest cover changes on the climate in the USA (Bonan 1997). And the cooling was also observed in a simulation using a nested mesoscale model in northeast Colorado (Chase et al. 2000) and in the central plains. In addition, experiments with the Hadley Centre Climate Model (HadCM3) with prescribed SST showed that historical vegetation cover change results in a reduction in midlatitude annual mean temperatures within the model. And extreme scenarios over Amazonia replacing tropical forests with grass lead to warmer, drier climates in several studies (Sud et al. 1996; Bonan 1997). Since 1990s, numerical simulations of impact of vegetation changes on climate in China or East Asia have been conducted by Chinese scientists; results showed that the regional temperature, precipitation, and other indicators have been obviously influenced by the change, which could even affect the summer monsoon intensity of Asia in the heavily changed regions (Jin et al. 2010). However, due to the various scales and degrees of forestland and grassland change and different models that had been used, the simulation results were in poor comparability. Meanwhile, the limited calculation condition has shorter integration time of simulation, and the result cannot reflect the long-term climate effect triggered by the change, especially the medium- and long-term climate effects in the future.
How to find a systematic quantitative way to explore the future climate effects caused by the conversion from grassland to forestland? The comparative model experiments need to be carried out. In this section, we used the WRF model to quantify the regional climate effect triggered by the conversion from grassland to forestland in Fujian Province of southeast China. Based on the RCPs scenario data, future land transition of forestland from grassland in the study area was simulated by using dynamics of land system (DLS) model, and then, the space and timescales of regional climate effects were analyzed.
Data and Methodology
Study Area
The southeastern coast of China is one of the top-level regions with abundant water, heat, and sunlight resources. It plays an important role in the globalization and the Pacific Rim economic circle in China, which occupies about 5.33 % of the total land area, accounts for about 21 % of the national population, and creates 35.7 % of national GDP and 70 % of the total import and export of China. With the development of economy and the policy implementation such as “returning farmland to forest” ecological engineering project, the area of forestland expanded sharply, especially in Fujian Province, which is the most typical afforestation region in China. The forest coverage rate of Fujian is the highest in China, reaching 62.96 % in 2005. In addition, Fujian is the main region of conversion of forestland from grassland in China (Liu et al. 2010), and the conversion from grassland to forestland is obvious (Fig. 5.7). Statistical analysis indicated that during 2000–2008, 11.2 % of the grassland had been converted into forestland, accounting for 73 % of the total area of forest expansion. Besides, the dominated humid middle and south subtropical maritime monsoon climate, with various heat resources and plenty of water resources, played an auxiliary role in the conversion process. In 2005, the forest coverage rate in Fujian had reached 62.96 %, which was one of the highest forest coverage rates in the nation. In addition, the most part of grassland in Fujian Province is the secondary degenerative environment, which evolves from wasteland after the forest system damaged, and thus, it is beneficial for the conversion from grassland to forestland.
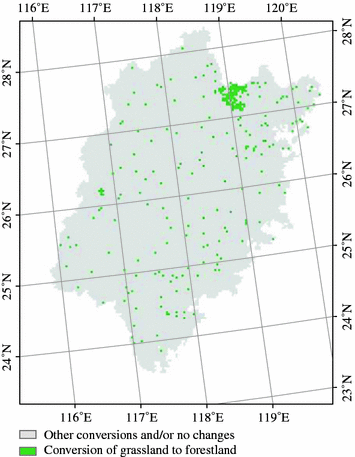
Fig. 5.7
Pattern of the conversion (measured in 3 km) from grassland to forestland in Fujian Province, 2000–2008
Data Sources
The lateral boundary force data were mainly derived from NCEP FNL and NCEP/NCAR reanalysis datasets. Forecasting data were derived from the multimodal data of WCRP’s Coupled Model Intercomparison Project Phase 5 (CMIP5). Chinese National Climate Center had finished the downscaling work of multimodal simulation datasets, which was unified to the same resolution and had been used to undertake the numerical simulation in the eastern Asia. The weighted average reliability value was used to undertake the multimodel ensemble (MME); then, the annual and monthly average data were made for 2000–2050, namely climate change forecast dataset in China. Data resolution was 1° × 1°, which only included the continental land, with a spatial scale of 15.5°–55.5°N and 72°–135°E.
Land cover data were extracted from the Chinese subset of the global land cover characteristics database which was developed based on Landsat TM scenes for 1999/2000 and the Chinese subset of the MODIS land cover data product in 2008. The two datasets have the spatial resolution of 1 × 1 km2 and an overall accuracy of 81 % (Liu et al. 2003b). DLS simulation requires spatial data of natural environment conditions such as climate, elevation, slope, plain area percentage, soil properties, and the geographic data, and thereinto, RCPs data were derived from land use harmonized data products (http://luh.umd.edu/data.php), and the climate observation data were acquired from records of 23 weather stations of the National Meteorological Information Center of China, including the moderate average annual rainfall during 2000–2008. Data about slope, aspect, and plain area ratio were extracted from elevation data based on 1 : 250,000 digital elevation model (DEM) for each 1 × 1 km2 grid. Soil property data came from the Second National Soil Census, and by using Kriging interpolation method, the spatial distribution of soil property was acquired. Regional condition data included the distance of each grid center to highway, provincial highway, main roads, and the provincial capital, which were calculated by distance measuring tools based on the national 1 : 250,000 fundamental geographic maps.
Estimation Model of Climate Effects
The regional influence of the conversion from grassland to forestland could be described by effect index (EI), which is defined as follows:
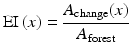where x is any meteorological parameter such as annual average temperature, precipitation, water vapor mixing ratio, or wind speed. A change(x) is the grid number within the region where x is changed, A forest is the grid number of the area converted from grassland to forestland, both of them are calculated at the regional scale, and a bigger EI reflects a higher efficiency of its climate effect.
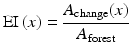
We used two nested grids with the spatial resolutions (grid numbers) of 3 km (162 × 177). The vertical grid consisted of 35 full sigma levels from the surface to 100 hPa, of which the lowest 13 levels were below 1 km to show a finer resolution in the planetary boundary layer. Both the initial and the boundary conditions with a resolution of 1.0° × 1.0° were from the National Centers for Environmental Predictions. The simulations were divided into two stages. Firstly, simulation was integrated for 8 years from January 1, 2000, to December 31, 2008. The initial 15-day period was considered as a spin-up period to minimize the effect of the initial conditions. In the control experiment, the land cover data were updated from the 2008 MODIS satellite observations to represent current land cover conditions (TFG case). For the sensitivity experiment, all newly expanded forest cover from grassland during 2000–2008 in domain 2 was replaced by grassland, which is the most common land cover type surrounding the forest area in the simulated domain (NOTFG case). These two cases were compared to analyze the influence of historical conversion from grassland to forestland (2000–2008) in Fujian. Secondly, we were moving on to the future stage, which was simulated from January 1, 2010, to December 31, 2050, and based on the hypothesis that the future climate effect simulation of the land use and land cover change would be reliable as that of the historical one, the newly expanded forestland from grassland was updated from the results of DLS simulation to represent the future forestland transition from grassland in the NOTFG case. The parameterization schemes used for the two stages are as follows: Noah land surface processes, CAM3 radiative scheme, WSM3 simple ice microphysics scheme, Grell 3D cumulus convection schemes, and YSU boundary layer scheme.
Simulation Model of Land Transition
Based on the conversion data under the RCP6 and RCP8.5, which were produced by AIM and MESSAGE model from 2009 to 2050, respectively, the total area of land transitions from grassland to forestland was calculated from 2010 to 2050. They were used by DLS to simulate the future spatial pattern of the conversion of forestland from grassland in Fujian. The DLS model is theoretically based on restrictions of the distribution of land types. It dynamically simulates the macroscopic pattern changes in land cover by classifying the driving factors that influence this pattern. Considering the links among related models of nature, ecology, and economy, we used DLS to spatially allocate the area change in the forestland transition from grassland. Based on the spatial statistics data, the probabilities of the transition of grassland to forestland and the probabilities of the distribution of this transition were predicted at the pixel level. In the simulation process, we also considered the influence of macroscopic factors such as topography, environment, trade, and institutional arrangement and land management policies to more accurately simulate possible scenarios of pattern changes in land system (Deng et al. 2006b).
Scenario Building and Data Analysis
We took RCP6 as the moderate development scenario of Fujian; it is a stabilization scenario where total radiative forcing is stabilized after 2100 without overshoot by employment of a range of technologies and strategies for reducing greenhouse gas emissions. Grassland area declined, while total forested area extent remained constant throughout the century at the global scale.
While RCP8.5 is an emission pathway which reaches a radiative forcing of 8.5 W/m2 and rising in 2100, we made it a fast development scenario of Fujian, with a high magnitude of climate change and factors related to higher vulnerability (e.g., higher population growth and lower levels of economic development). It is characterized by increasing greenhouse gas emissions over time representative for scenarios in the literature leading to high greenhouse gas concentration levels. The underlying scenario drivers and resulting development path are based on the A2r scenario. An important feature of the RCP8.5 was the increase in cultivated land by about 185 million hectares (Mha) from 2000 to 2050; forest cover declined over the century by 300 Mha from 2000 to 2050.
The transition from grassland to forestland in Fujian is significant under the RCP6 and RCP8.5 scenarios with a spatial resolution of 0.5° × 0.5° (Fig. 5.8). Firstly, the downloaded data were downscaled to 1 × 1 km2 grid, and then, the overlay analysis was taken with the administrative boundary data to calculate the total amount of the transition from grassland to forestland. During 2010–2050, the transition of forestland from grassland presents a soaring trend in 2010–2020, followed by a sharp decline in 2020, when a stable decrease occurs in the next 30 years under the RCP6 scenario, but it is pervasively higher than that of RCP8.5.
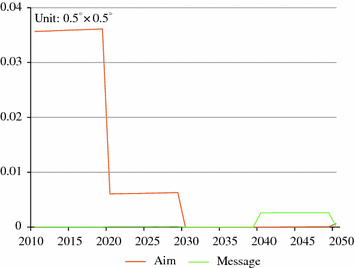
Fig. 5.8
Conversion from grassland to forestland under the RCPs scenarios in Fujian Province, 2010–2050
Results
Impact on Temperature
Temperature differences of near-surface temperature in 2 meters height (T 2m) of forestland conversion from grassland and non-conversion experiments show the climate effect of the conversion (Fig. 5.9). In summer, the cooling effect has emerged in the conversion area of grassland to forestland. Compared with the other area, the maximum difference of the seasonal average T 2m is approximately 0.60 °C in the conversion area of grassland to forestland, and the regional average T 2m decreases by 0.16 °C with EI(T 2m) = 2.23. While in winter, there is a heating effect in the conversion area of grassland to forestland, with the maximum difference of the seasonal average T 2m increasing by 0.08 °C, and the average T 2m is rising by 0.03 °C with EI(T 2m) = 1.93. On the whole, the annual average T 2m decreases by 0.11 °C in Fujian.
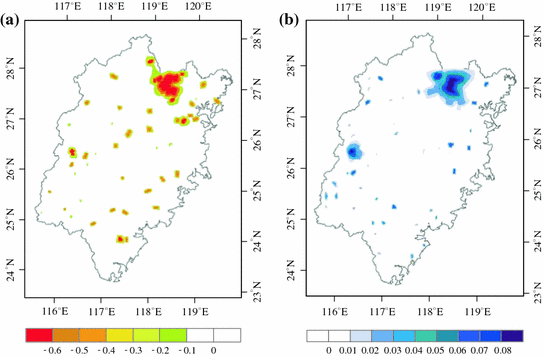
Fig. 5.9
Seasonal difference of near-surface temperature at 2 m height (unit °C) in the experiment of conversion from grassland to forestland in Fujian Province, 2000–2008. Panel a and Panel b identify the temperature difference in summer and winter, respectively
Impact on Precipitation
Precipitation varies from one region to another (Fig. 5.10), the northwest Fujian was the main area where the amount of precipitation increased, while the southeast reverse the case. According to the spatial statistical analysis, the range of the difference of precipitation between TFG case and NOTFG case is −40 to 70 mm, and the majority of the change ranged from −30 to 50 mm, while the annual average precipitation increased by 46 mm with EI (P = 4.68).
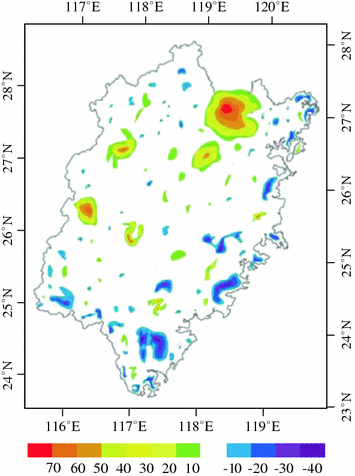
Fig. 5.10
Annual average precipitation difference (unit mm) in the experiment of conversion from grassland to forestland in Fujian Province, 2000–2008
Validation of the Control Case
We selected 23 meteorological stations’ continuous observation data from 2000 to 2008; all of them have passed the homogenization test. The monthly mean temperature data are provided by the National Meteorological Information Center of China. When assessing its simulation capability, the simulation results were bilinearly interpolated to 23 weather stations, to calculate the average and seasonal temperature of each site.
The errors between the simulations and observations of surface temperature and precipitation are listed in Table 5.3, and the P test values are 0.81 and 0.76, respectively. The errors between the simulations and observations are less than 1.00 °C except for the Qixianshan, Jianyang, Ningde, Shanghang, and Longyan stations. The relative errors of the annual precipitation are all less than 12 %; therefore, we think that the simulation result is reliable and presume that it will work accordantly well in the future.