Appeal to Expert Testimony – A Bayesian Approach
By the aid of Bayes’ theorem, we can calculate the probability (P) of a hypothesis (H) given some evidence (E). We can therefore use the formula to update our belief in a hypothesis after considering new evidence. The usefulness of the formula is today widely acknowledged. In the argumentation context, it has proven capable of accounting for several informal fallacies (Korb 2003; Bender et al. 2007) and promises to be a generally useful tool for the analysis of argumentation, including source reliability and appeal to expert opinion (Schum 1975; Goldman 2001; Hahn et al. 2009, 2013).
In this article, we will use Bayes’ theorem to assess how the probability of a hypothesis (H) is influenced by the fact that an expert claims that the hypothesis is true. In our analysis, the evidence (E) consists in the expert’s testimony that H is true, and the left-hand side of the formula, P(H|E), is the probability that the hypothesis is true given that the expert says so. To calculate this probability with Bayes’ theorem we need to know three things:
1.
P(H), The probability that the hypothesis is true before considering the expert’s testimony. This probability is referred to as the prior probability.1 From here, we can derive the prior probability that the hypothesis is false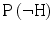 
, which also appears in the formula, by applying the negation rule, 
,
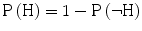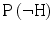, which also appears in the formula, by applying the negation rule, 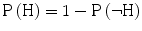,2.
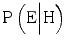, The probability that the expert would testify that the hypothesis is true, given that it is true. This is the probability of a true positive.
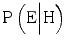, The probability that the expert would testify that the hypothesis is true, given that it is true. This is the probability of a true positive.3.
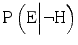, The probability that the expert would testify that the hypothesis is true, given that the hypothesis is actually false. This is the probability of a false positive.
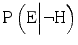, The probability that the expert would testify that the hypothesis is true, given that the hypothesis is actually false. This is the probability of a false positive.In the theorem’s terminology, the evidence (the expert’s testimony that the hypothesis is true) increases the probability that the hypothesis is true when ![$$ \mathrm{P}\left(\mathrm{H}\Big|\mathrm{E}\right)>\mathrm{P}\left(\mathrm{H}\right) $$
” src=”/wp-content/uploads/2015/10/A320960_1_En_1_Chapter_IEq5.gif”></SPAN>. This situation occurs if it is more probable that the expert testifies that the hypothesis is true when it is true, than when it is false, i.e. when <SPAN id=IEq6 class=InlineEquation><IMG alt=]()
\mathrm{P}\left(\mathrm{E}\Big|\neg \mathrm{H}\right) $$
” src=”/wp-content/uploads/2015/10/A320960_1_En_1_Chapter_IEq6.gif”>. By convention, these two probabilities, 
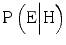and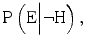 
are referred to as likelihoods. How much the probability 
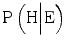increases depends on how large the difference between the two likelihoods is, as well as on the size of the prior probability P(H). If, on the other hand, 
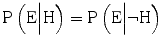, the probability of the hypothesis is unaffected by the expert’s testimony. The strength of the evidence is therefore measured as the likelihood ratio (LR), in the following way:
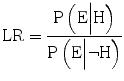If 
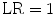, the expert testimony has no effect on the probability. And, in the strange but not impossible case that 
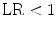the expert testimony lowers the probability that the hypothesis is true. The likelihood ratio is hence a measure of the diagnosticity of the expert testimony.
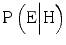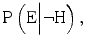and are referred to as likelihoods. How much the probability 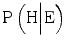increases depends on how large the difference between the two likelihoods is, as well as on the size of the prior probability P(H). If, on the other hand, 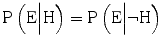, the probability of the hypothesis is unaffected by the expert’s testimony. The strength of the evidence is therefore measured as the likelihood ratio (LR), in the following way: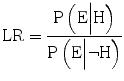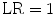, the expert testimony has no effect on the probability. And, in the strange but not impossible case that 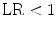the expert testimony lowers the probability that the hypothesis is true. The likelihood ratio is hence a measure of the diagnosticity of the expert testimony.In the next section we will discuss how factors that relate directly to the expert’s reliability affect the likelihood ratio, and thereby the probability that a hypothesis is true, given that an expert says so. With the aid of Bayes’ theorem, we can clarify how important these factors are, and to what extent they should affect our decision to trust, or not trust, an expert. It is interesting to note that many experts and other scientists make similar evaluations of their own diagnostic tools. For example, a physician who wants to calculate the probability that a person with a positive biopsy suffers from cancer needs to consider the probabilities of true and false positive test results as well as the prior probability of the disease. Just like the physician uses medical knowledge and Bayes’ theorem to arrive at her conclusion, the layman can use expertology and Bayes’ theorem to evaluate the reliability of the expert’s conclusion. In this way, expertology and Bayes’ theorem allow us to assess the diagnosticity of expert testimony as an instrument in a way that complements the expert’s evaluation of her own instruments.
1.6 Assessing Arguments that Question the Expert’s Reliability
As we have seen, an appeal to expert testimony can be met by counter arguments that cast doubt on the expert’s competence or motivation. It goes without saying that deficiency in competence or motivation should decrease our trust in an expert’s testimony. It is less obvious by what mechanisms changes relating to these factors affect the evidentiary value of the testimony, to what extent they do so, and how these changes should influence our actions. The answers to these questions are in part empirical, but also have a mathematical dimension, which must not be neglected. In this section, we will discuss some of the insights that Bayes’ theorem can give us to these questions.
As we have seen, the evidentiary value of the expert testimony is reflected by the likelihood ratio,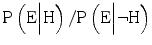 
. If the expert has insufficient competence, the likelihood ratio will decrease. The magnitude of the decrease, and the mechanisms underlying it, depend on the expert’s awareness that her competence is insufficient, as well as on her cautiousness to avoid incorrect statements. For example, lack of competence in combination with lack of awareness/cautiousness will strongly increase the probability that the expert erroneously claims that the hypothesis is true, 
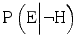. Insufficient competence in combination with awareness and cautiousness, on the other hand, will normally not have this strong effect on 
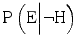, since the expert who realizes that her competence is insufficient will be inclined to say that she is unable to judge whether the hypothesis is true or false. If the expert is extremely cautious, insufficient competence could, theoretically, decrease both 
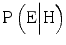and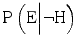 
but the combined effect remains a decrease in evidentiary value, as long as 
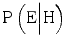decreases more than 
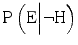. How people react when they have insufficient competence is an empirical question. Here, we will make the assumption that extreme awareness/cautiousness or unawareness/incautiousness are rare and that insufficient competence therefore typically makes the expert more prone to say that H is true when it is false and less prone to say that H is true when it is true. In other words, we will assume that insufficient competence typically increases 
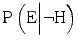and decreases 
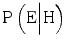. Since the numerator of the likelihood ratio (LR) in this situation decreases and the denominator increases, LR will decrease accordingly.
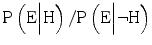. If the expert has insufficient competence, the likelihood ratio will decrease. The magnitude of the decrease, and the mechanisms underlying it, depend on the expert’s awareness that her competence is insufficient, as well as on her cautiousness to avoid incorrect statements. For example, lack of competence in combination with lack of awareness/cautiousness will strongly increase the probability that the expert erroneously claims that the hypothesis is true, 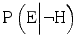. Insufficient competence in combination with awareness and cautiousness, on the other hand, will normally not have this strong effect on 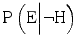, since the expert who realizes that her competence is insufficient will be inclined to say that she is unable to judge whether the hypothesis is true or false. If the expert is extremely cautious, insufficient competence could, theoretically, decrease both 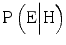and 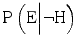but the combined effect remains a decrease in evidentiary value, as long as 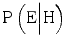decreases more than 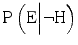. How people react when they have insufficient competence is an empirical question. Here, we will make the assumption that extreme awareness/cautiousness or unawareness/incautiousness are rare and that insufficient competence therefore typically makes the expert more prone to say that H is true when it is false and less prone to say that H is true when it is true. In other words, we will assume that insufficient competence typically increases 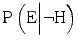and decreases 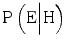. Since the numerator of the likelihood ratio (LR) in this situation decreases and the denominator increases, LR will decrease accordingly.To illustrate, let us consider a case where we initially perceive the expert to be highly competent and estimate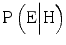 
at 0.90 and 
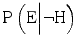at 0.02. Under these circumstances 
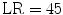. What this means for 
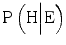depends, of course, on the prior probability P(H). Let us assume as an example, that 
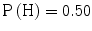(given the evidence that we had taken into count prior to the expert’s testimony). In this case, the probability that the hypothesis is true given that the expert says so is approximately 0.98. Now, suppose that we learn that the expert is less competent than we first thought. It turns out that the expert lacks practical experience. Due to the expert’s insufficient competence, we find it reasonable to adjust 
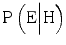from 0.90 to 0.80 and 
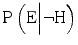from 0.02 to 0.20. With these modified likelihoods, the likelihood ratio drops from 45 to 4, and the probability that the hypothesis is true, given that the expert claims that it is true, drops from 0.98 to 0.80. The new information has significantly lowered the evidential value of the expert’s testimony (Table 1.1).
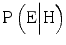at 0.90 and 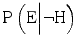at 0.02. Under these circumstances 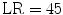. What this means for 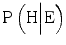depends, of course, on the prior probability P(H). Let us assume as an example, that 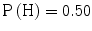(given the evidence that we had taken into count prior to the expert’s testimony). In this case, the probability that the hypothesis is true given that the expert says so is approximately 0.98. Now, suppose that we learn that the expert is less competent than we first thought. It turns out that the expert lacks practical experience. Due to the expert’s insufficient competence, we find it reasonable to adjust 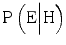from 0.90 to 0.80 and 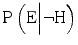from 0.02 to 0.20. With these modified likelihoods, the likelihood ratio drops from 45 to 4, and the probability that the hypothesis is true, given that the expert claims that it is true, drops from 0.98 to 0.80. The new information has significantly lowered the evidential value of the expert’s testimony (Table 1.1).Table 1.1
Insufficient competence
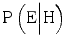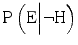 |  | LR |  | |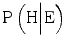
|---|---|---|---|---|
Competence | 0.90 | 0.02 |  |  |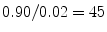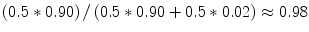
Insufficient competence | 0.80 | 0.20 | 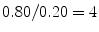 | 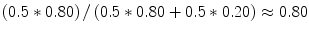 |