Valuing Maritime Investments with Real Options: The Right Course to Chart

Chapter 24
Valuing Maritime Investments with Real Options: The Right Course to Chart
Helen Bendall*
1. Introduction
Real option analysis (ROA), an extension of discounted cash flow (DCF), has at its core the calculation of shareholder value and thus is a very powerful metric to value maritime investments. The basic principles underlying real options are intuitively appealing and readily understood by management, having been used for millennia. The first recorded real options deal being that of the philosopher and mathematician, Thales of Miletus (circa 624BC–536 BC) who made a fortune by taking an option on renting olive presses in Miletus and Chios in Asia Minor at a set price and the crop turned out to be bountiful.1 Their intuitive appeal led Copeland and Antikarov (2001), to predict that by the end of the first decade of the second millennium AD that real option analysis, ROA, would become the standard valuation metric. It is indeed true that most mainstream academic finance texts now include real option analysis as a tool for investment evaluation but perhaps we are still a little distance off from the analysis achieving “standard” investment evaluation status. Others (Triantis and Borison, 2001 amongst many) suggest that it is the process and discipline of framing an investment decision in real options terms that provides the greatest benefit. If used as a conceptual tool, it allows management to characterise rather than calculate and communicate the strategic value of an investment project. Real options helps managers formulate their strategic options (Amram and Kulatilaka, 2000) enabling investment strategy to be crafted as a series of options that are continually being exercised to achieve both short and long term returns on investment (Yeo and Qui, 2003). The real option method enables decision-makers to leverage uncertainty and limit downside risk. In this current period of heightened business uncertainty ROA offers managers a very useful and an appropriate approach to evaluate investments and formulate strategy.
A discussion of the key issues of valuing investment in an uncertain world follows in Section 2 with real options analysis, ROA, offered as an alternate paradigm as it allows managers the ability to alter/adapt the project in light of new information. Various applications of real options in the maritime industry are used to illustrate the scope and applicability of an option approach. Real options are embedded in most projects but there has been a certain hesitation by management to forego their traditional DCF “comfort zone”. This is somewhat surprising as ROA should not be viewed as a revolutionary approach but evolutionary as it extends traditional DCF analysis. Section 3 reviews the reasons for this view and outlines and discusses several ROA methodologies. Section 4 demonstrates ROA by illustrating the power of the technique in specific maritime case studies involving new technology. Section 5 concludes the chapter.
2. Valuing Investments
2.1 Limitations of traditional DCF
Conventional DCF analysis for project evaluation is taught extensively in business schools and is used by a majority of firms.2 It appears that many academics and executives, by implementing investment decisions based solely on traditional capital budgeting techniques or by focusing on narrowly defined problems may have failed to take into account uncertainty and the flexibility to alter or adapt projects once begun. Often there is a lack of understanding as to how to include strategic issues in an analysis. This is not to say that mangers have not recognised that the failure to do so can lead to costly errors, but the difficulty of such planning leads many to ignore the potential costs and hope that serious problems do not arise (Teisberg, 1995). Managers must be able to include uncertain future outcomes and potential strategic responses in a prospective analysis of a capital investment project.
Because of its inflexibility and the failure to take into account strategic or competitive issues, DCF criteria may undervalue investment opportunities, leading to lack of investment and loss of competitive position. Dissatisfaction with traditional DCF led some to propose that the problem was simply a misuse or misapplication of the underlying theory (Hodder and Riggs, 1985) or move strongly that DCF was an inappropriate valuation method. Hertz (1964). Magee (1964) suggested instead the use of simulation and decision trees, or Decision Tree Analysis (DTA) as a means to capture the value of future operating flexibility associated with many projects. Other academics and company executives wanting to refine DCF have turned their attention to technical questions related to the selection of the risk-adjusted process without considering adequately the appropriateness of DCF for valuation of particular projects which have strategic implications. The traditional DCF approach cannot fully accommodate the interdependencies between current and uncertain or contingent future decisions which make the risk-adjusted discount rate non-deterministic.
Traditional DCF is based on value maximisation under passive or static conditions and on implicit assumptions concerning a predetermined operating strategy in which the project would be initiated immediately and operate continuously at base case until the end of a pre-specified useful life. Ansoff (1965) and Myers (1987) point out that traditional capital budgeting techniques are unable to forecast the value of projects not yet in hand and that they are difficult to use in situations involving multiple objectives or substantial project interdependencies e.g. synergies or other unique qualitative attributes (Lai and Trigeorgis, 1995). The standard NPV although perfectly suitable for projects that once undertaken require no further decisions or actions by the firm, is of little assistance in the valuation of projects which offer managerial flexibility in dealing with future contingencies. In summary, DCF may be appropriate when applied to narrowly defined problems but is inadequate when uncertainty and strategic considerations are paramount (Pinches, 1982, Myers, 1987 amongst many). These observations point to the existence of an extra parameter which managers implicitly or explicitly factor into their investment decisions.
Well before the development of Real Options Analysis, ROA, managers and strategists intuitively adjusted their investment strategies to include other factors such as future growth considerations, realising that traditional DCF criteria undervalued many investment opportunities. Kester (1984) developed Myers’ (1977) concept of thinking of discretionary investment opportunities as “growth options”. These embody both strategic and competitive elements. For example, shipping lines may enter a new market or trade not so much because the immediate investment generates a positive NPV, indeed it may be the opposite, but in order to keep a competitor out of the trade or to put the line in an advantageous position for valuable follow up opportunities. An investment such as this is an example of a multistage decision that involves “real” options. The decision to enter the trade has the ability to create future assets (cash flow) as a by-product of the initial investment decision. The shipping line, by undertaking the initial investment, has the option in future to expand the number of ships in the trade, or exit the trade depending on market circumstances in the future.
2.2 Real options
Real options capture the value of managerial flexibility to adapt decisions in response to unexpected market developments, giving the manager the right to defer, to expand, to contract or abandon the project once more information becomes available. Companies create shareholder value by identifying, managing and exercising real options associated with their investment. The concept is similar to financial options.3 An option gives the right but not the obligation to undertake an action i.e. a business decision, at a predetermined cost (the exercise price), for a predetermined period of time (the life of the option). A call option is the right to buy the underlying asset at the predetermined (exercise) price. As there is no obligation on the part of the holder of the option to exercise the call, the option can lapse. However if the option is exercised then the profit on the option is the difference between the value of the underlying asset and its exercise price. A put option is the right to sell the underlying asset to receive the exercise price and thus is the opposite of a call. A European option can only be exercised on its maturity date where as an American option can be exercised at any time during its life and thus is more applicable to investment in real assets. An option is in the money, i.e. profitable to exercise if the price of the underlying asset is above the exercise price with a call option and below the exercise price with a put option. If not profitable to exercise it is out of the money.
Although examples of real options have been recorded throughout history, the first to coin the term “real options” was Myers (1977), who applied financial option pricing theory to the valuation of a non-financial or “real” investment in a multi-stage manufacturing plant expansion. Other academic papers followed but it was not until the last 10 years that interest in ROA began to attract considerable attention from corporates as a potentially important tool for valuation and strategy (Borison, 2005). ROA has been adopted by a number of organisations in the transport, energy, infocom and mining industries as well as large consumer and industrial companies, particularly those engaged in R&D and involving a multi-stage production process (Triantis and Borison, 2001).
Real options are often classified by their flexibility. If management wants to scale up production then management needs to value an option to expand. They would need to value an American call which gives them the right but not the obligation to add additional capacity to their current project by further investment at a later date. In contrast to scale down an operation or to close an operation are examples of American put options where management has the right to sell, but not the obligation, should the operating environment worsen. An option to contract allows management to sell a fraction of the operation while an option to abandon at a fixed price leads to closure for a predetermined salvage value. Being allowed to defer the decision to invest is an option to defer while switching options are portfolios of American puts and calls which allow the flexibility to switch inputs or outputs. Compound options are options on options and point to the need for sequential investment decisions while rainbow options reflect multiple sources of uncertainty.4
2.3 A taxonomy of maritime real options5
2.3.1 Option to expand
Perhaps one of the easiest real options to identify is the option to accelerate the rate or expand the scale of operation by investing an additional outlay. Once established in a trade, for example a shipping line can increase the number of vessels in a trade, should market conditions warrant. This ability to make a discretionary investment is similar to an American call option on the increased scale of the project and with the exercise price, the additional outlay. The project then can be seen as the base scale project, or static NPV, plus a call option on the future investment, which is the value of flexibility. The option becomes profitable to exercise, if future demand turns out to be higher than expected. A major source of value from infrastructure investments arises from the ability to enhance the upside of a project during good market conditions by making follow-on investments (Myers, 1977). Ports with surplus land can build extra terminals and terminal operators can increase the number of gantry cranes on a berth. This option, which will be exercised only if future market developments turn out favourably, can make seemingly unprofitable investments (based on static NPV base-case) worth undertaking. Infrastructure investments consist of both tangible and intangible core assets on which individual operating flexibility options are based. Flexible computer-based manufacturing systems, such as CAD-CAM manufacturing in the ship building industry, are evidential. Investment in training has intangible option benefits for ship and port operators if for example the management has a multi-skilled workforce to utilise.
2.3.2 Growth options, strategic options, competitive options
Growth options are similar to expansion options but with more emphasis on strategic or competitive positioning. They set the path for future opportunities. Growth options are possible because of the firm’s ownership of intangible assets such as patents, proprietary technologies, ownership of valuable resources, managerial capital, reputation or brand name, scale and market power which allow companies to grow through future profitable investments and to more effectively respond to unexpected adversity or opportunities in a changing technological competitive or general business environment (Trigeorgis, 2000). The ownership of growth options enhances management’s flexibility for future action and gives the firm a sustainable competitive advantage.
Technological superiority and know-how permit further sequential (or parallel) developments ensuring competitive edge is maintained. In this way growth options such as in this example are called complex or compound options as growth comes from exercising a series of options (i.e. an option on an option). For the shipbuilding and related industries, R&D investment is essential in a competitive environment with rapid technological developments. Australian shipbuilders became world leaders in aluminium welding techniques and design of high-speed craft which ensured that they remained ahead of other competitors by continual design development. Thus the development of first generation product can create a proprietary growth option acting as a springboard for developing in the future lower cost and improved design or indeed new applications. Investment in Information Technology (IT) can be viewed at a growth option as it provides a link in the chain to interrelated projects and growth opportunities.
Similarly development of a new market/trade with an initial negative NPV can open up or generate opportunities in other markets at a later stage or can pre-empt the entrance of a competitor. This investment may be viewed as a strategic investment. Strategic acquisitions such as purchase of a terminal by a shipping company gives the shipping line control over competitor access and timing to the facilities conferring on the company a competitive edge via the proprietorial real option.
Once investment opportunities are properly seen as collections or a portfolio of real options, strategic planning can be more readily viewed as involving the explicit recognition, creation and management of current and future investment opportunities (Lai and Trigeorgis, 1995). Examples taken from Bendall and Stent (2005, 2007a) are used below in Section 4 to demonstrate how real options can be used to value complex maritime investment applications involving both mutually exclusive and non-mutually exclusive investment strategies.
2.3.3 Option to contact, option to abandon
Investors may also have embedded options to contract or abandon if a project fails to achieve the required rate of return envisaged, due to less favourable market conditions. If market conditions are weaker than originally anticipated management can operate below capacity or even reduce the scale of operations and thus save part of planned investment outlays as well as reducing operating costs. This flexibility to lessen the loss is analogous to a put option on part of the base scale project with the exercise price being equal to the potential cost savings. The option to contract is particularly valuable in the case of entering into a new market (trade) or in choosing among technologies with different construction to maintenance cost mix. To illustrate this point, management may chose initially a lower cost asset with higher maintenance expenditures in order to acquire the flexibility to contract operations by cutting down on maintenance if market conditions worsen.
If the project suffers severe losses through a systemic market decline or for some other reason such that the firm can no longer sustain its fixed costs then the project should be shut down. The more general purpose the capital asset (i.e. lower asset specificity, the higher will be the value of the abandonment option). For example a container ship or bulk ship would be considered to have low asset specificity while a gas carrier would have high asset specificity. This real option is equivalent in this case to an American put option. The underlying asset is the current value of the vessel where the salvage value is the exercise price.
In contrast infrastructure companies’ abandonment options may be less valuable than that of shipping lines because of the sunk cost nature of the assets. This means that their exercise price is low. Once constructed a port or terminal cannot be moved to another location or may not be profitably used for another purpose, although port land can be turned over to recreational use. With low exercise prices, the options and the business that own them would be worth less than they would otherwise.
2.3.4 Option to switch (output or input), location options
Product or input flexibility is a valuable option for management. With an option to switch, management can change the output mix (product flexibility) if prices or demand change or alternately, the same output can be produced using different types of inputs (input flexibility). For instance, Kulatilaka (1993) found that the value of the flexibility provided by an industrial dual-fired steam boiler that can switch between alternative energy inputs (natural gas and oil), as relative prices fluctuate, far exceeded the incremental cost of a single-fuel alternative. In fact, because of the existence of the switch option, the firm should be willing to pay a positive premium for flexible technology over a rigid alternative that confers no or less choice.
In the maritime industry there are many examples where management has opted for technology which allowed flexibility in output (product switch option) or choice of inputs (input switch option). In the 1970s a cement carrier was introduced into service on the Australian coast which could switch between diesel and compressed natural gas. In a greener world, the ability to use renewable resources to power vessels has been welcomed. The Solar Sailor can switch between wind, solar and diesel-electric power sources or can use a combination of all three, depending on weather conditions. New vessel designs are incorporating sail features allowing operators the option to save fuel by supplementing wind power Many ports/terminals opt for more expensive technology which allows flexibility in output (output switch) e.g. cranes with flexibility to service both panamax and post-panamax vessels. These investments may appear expensive at the time of purchase but the true valuation has included a (product or input) switch option.
Closely linked to switch options are location options. Multinational manufacturing firms are sensitive to changes in exchange rates and switch production inputs to choose, ex-post, the lowest input mix (input switch option) (Kogut and Kulatilka, 1994). Companies, such as Nike have moved production sites from one country to another to reduce costs and maximise profits as exchange rates, labour costs and investment incentives change. Shipping is a service industry sensitive to exchange rates and exchange rates may affect export competitiveness. The changing pattern of trade changes the demand for shipping services. However vessels can be re-routed or positioned in a new trade. Ships, in contrast to other capital intensive investments, usually have low asset specificity (Bendall and Manger, 1991) and can be switched (output switch) easily to a new trade. A vessel owner has thus acquired a valuable switch option which is nested in the initial cost of the ship.
2.3.5 Option to defer or waiting to invest or timing options
An option to defer is an example of an American call option with its exercise price the money to be invested at a later date. It can be found in most projects where one has the right to delay the start of the project. If a shipbuilder holds a patent for new technology, the builder can delay marketing the new design until market conditions prove more favourable or has sold existing vessels with older technology currently under construction. A deferral option is often at the heart of real option flexibility value because it can be linked to other options. Being able to postpone a business decision to expand, to contract, to change inputs or outputs, to abandon etc until more information is available is extremely valuable to management. A project with a negative NPV may become profitable if it can be deferred over a certain time period. If a ship operator acquires a controlling interest in a port/terminal in a different trade he can chose if and when his ships will use the facilities, safe in the knowledge that he will take priority at the berth over competitors in the future and thus the opportunity to enter and control that trade. If the firm chooses to invest “now” rather than invest “later” the NPV must be raised to offset the loss of the timing option (Dixit and Pindyck, 1994). This is in contrast to the expansion or growth opportunities where the option to expand makes up any shortfall in the static NPV.
A lease enables management to defer investment. If the fast ship/ferry operator had been able to obtain a time charter (an operating lease) or an option to buy (or an option on a financial lease) from the shipbuilder and was able to defer a commitment to purchase until there was more certainty regarding oil prices, or other market conditions then the ferry/ship operator would have acquired a valuable real option (to defer). Similarly a terminal may lease equipment before committing to buy, awaiting the necessary growth in throughput to make the investment profitable.
Time charters with purchase options, T/C-POPs, investment strategies offer the owner of the (call) option valuable flexibility. They are options to defer the decision to buy, but can be combined with a number of embedded options. In a European style T/C-POP the charter is given the opportunity to purchase the vessel at the end of the charter period at a pre-determined price while in an American T/C-POP the owner can opt to purchase the vessel at any time up before the expiry date.6 The value comes from the flexibility to choose if and when to buy the vessel (exercise the option) as uncertainty unfolds. T/C-Pops can be structured to give the holder a number of strategy choices. The T/C-POP holder may purchase of the vessel (exercising an expansion option) if buying is more advantageous to the ship operator than opting to continuing chartering or take on a new T/C-POP (i.e. deferring for another period) or indeed to abandon the trade altogether (an abandonment option).
2.4 The grantor of the real option
To encourage investment in infrastructure projects governments often grant real options to compensate for the sunk nature of the investment. This can be in the form of a revenue guarantee or clauses guaranteeing buy-backs at given prices. Shipbuilders may offer as a safety net or security to new investors/financial institutions an option to buy-back the vessel should the profitability of the venture fail. The buy-back is pre-set generally on a sliding scale at rates commensurate with depreciation and the time value of money. This is a great deal for the shipowner as the holder of the real option posses a valuable asset, but as grantor of the option the shipbuilder is bearing the risk as he takes on a contingent liability until the option lapses. Bendall and Stent (2007b) demonstrated how to value such “sweeteners” from the shipbuilder’s point of view.
3. Valuing Real Options
“Whether advocated in its strong form as a core valuation tool or its more moderate forms as a ranking tool, a heuristic or a metaphor, the appeal of real options lies in its promise of structuring decision making under uncertainty” (Adner, 2007).
While the argument that the advantage of ROA lies in its framing and structuring of the investment decision in real option terms has great allure, Damodaram (2005) advocates the importance of the strong form. He argues that if used only in a qualitative way that there is danger that the approach could be used to justify poor investments. Managers who argue for taking on a project with poor returns or pay a premium for acquisitions on the basis of embedded real options should be required to value these real options and demonstrate that in fact the economic benefits do indeed exceed the costs.
3.1 Real options analysis
As described in Section 2, the conceptional principles are similar to that of financial market options. The opportunity to put an additional ship in the trade is similar to an American call option and is the right but not the obligation to acquire a claim to the cash flow value. Similarly the right, but not the obligation, to reduce the scale of operation, say moving from two ships to one in a trade or exiting the trade altogether, is an example of a put option. ROA thus can correctly value managerial flexibility by explicitly considering appropriate action at future dates on which information about the project’s profitability is revealed. The project’s true valuation may look more attractive when the value of this flexibility is incorporated.7 This means that a project may have a static NPV that is negative and therefore would be rejected using traditional NPV rules but may be accepted if the value of flexibility is added.
Value of project with flexibility = Value of project without flexibility + Value of flexibility
Thus the value of the project is equal to the traditional static NPV or base case plus a value for active management. An option’s approach views capital investment as an on going process requiring active managerial involvement and ROA provides the means to value this flexibility at the ouset.
The quantitative origins of real options’ pricing derives from the financial markets with the seminal work of Black and Scholes (1973) and Merton (1973) in pricing financial options. The model was perceived to be complex and off-putting to many practitioners (Trigeorgis, 2000). Cox, Ross and Rubinstein’s (1979) binomial approach presented a more simplified methodology by evaluating financial options in discrete time.
Although the Black Scholes’ model is mathematically challenging and the assumptions necessary too restrictive for pricing of real options, the principles are useful in developing an understanding of real option valuation. The basic variables in their “closed form” financial option pricing model are the value of the underlying asset; the exercise price; the time to expiration of the option; the volatility (standard deviation) of the underlying risky asset and the risk free rate of interest over the life of the option.
In the case of a real option the underlying risky asset is the value of the investment or project. If the value of the project rises, so too would the value of the option. The exercise price is the amount needed to exercise the option i.e. the additional investment costs in a multistage project. Note that in the case of a call options, as the value of the exercise price increases, the value of the option decreases but increases the value of the option in the case of a put. As the time to expiration (maturity of the option) increases so too does the value of the option. This makes intuitive sense in situations where there is a great deal of uncertainty. Obviously the longer the time there is to delay the investment decision the more information is likely to become available. The value of the option is therefore sensitive to the degree of uncertainty or riskiness (volatility) of the underlying asset. Again this makes sense if we understand that the payoff of the call option depends on the value of the underlying asset exceeding its exercise price. This is more likely to occur if volatility increases. Lastly the value of the option increases if the risk free rate rises as it increases the time value of money advantage in deferring the investment cost until more information is known.
Cox and Ross (1976) recognised that an option could be replicated (to create a “synthetic” option) from an equivalent portfolio of traded securities. The replicating portfolio approach is based on the Law of One Price which simply states that to prevent arbitrage (riskless) profits, two assets with the same payoffs (“twin security”8 or “twin asset”9) in every state of nature are perfect substitutes (i.e. perfectly correlated) with the underlying risky asset and therefore have the same price (value). The risk-neutral probability approach is mathematically equivalent. A hedge portfolio is created, composed of one share in the underlying risky asset and a short position in “m” shares of the option being priced. The hedge ratio m is riskless as loss on the underlying asset is offset by the gain on the option (and vice versa) – hence risk free.
3.2 Risk neutral valuation example
The example, although simple, illustrates ROA valuation principles. It demonstrates how static NPV can underestimate the value of the project simply by not taking into account the embedded real option.
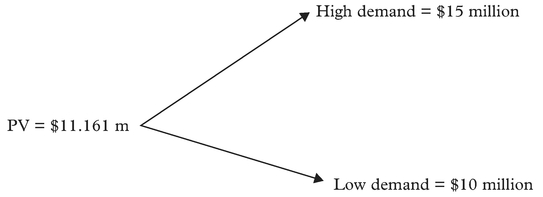
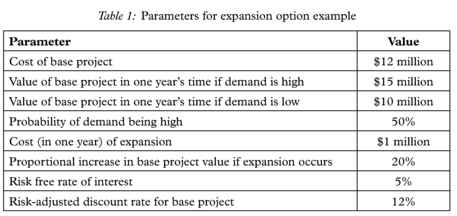
Assume that a firm is considering an initial investment costing $12 million. The value of the project in one year’s time is dependent on the (currently unknown) demand for the product or service. If demand turns out to be high, the project will be worth $15 million; if demand turns out to be low, the project’s value including the original investment would be only $10 million.10 These high and low outcomes are equally likely, i.e. each occurs with a 50% probability (a 50–50 chance). The present value, PV, was determined by multiplying the value of the high and low outcomes by the respective probability and discounting by the risk adjusted discount rate of 12%. See Figure 1. The risk free rate is 5%. The parameters are summarised in Table 1.
If the standard NPV analysis is applied by discounting the expected cash flows by the risk adjusted discount rate the base project’s present value is $11,161,000.
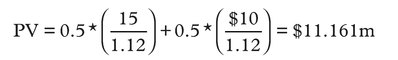
NPV = Present Value − Initial investment
= $11.161m − $12m
= – $839,000 → negative. Do not invest.
The NPV of – $839,000 is obtained by subtracting the initial capital cost of $12 million. In the absence of managerial flexibility (real options), the DCF analysis rule leads to a rejection of the project as acceptance would destroy value in the firm. This decision ignores the ability of management to alter the investment in response to new information. Traditional NPV is unable to capture the value of any embedded real option. Should demand conditions be more favourable than expected one year later, management would like the flexibility to expand (an expansion option). The traditional NPV analysis deals with this by implicitly assuming that management commits to a particular course of action (expand or not expand) at the time the project is launched, regardless of the conditions that subsequently prevail.