Rule-Following and Logic
(29.1)
If we remain within pure logic, LIR produce theorems from other theorems, ultimately from logical axioms. If A is a logical theorem, we write
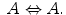
(29.2)
where the symbol ├ refers to the provability operator. Intuitively speaking, Eq. (29.2) says that A is a logical axiom or a theorem deduced from axioms. Consequently, logical theorems (axioms are a kind of theorems) are said to be inferred from the empty set of assumptions. Thus, the operator ├ magazines, so to speak logical inferential machinery.
What is the relation between ├ and ╞ (╞ A means ‘A is a logical truth’)? If a LOG is complete (I consider this property as a substantial feature of logic), we have
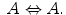
(29.3)
Thus, provability from the empty set of premises is equivalent to universal (logical) validity. Interpret logical rule-following as ‘obey rules collected by ├.’ Consider the implication
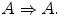
(29.4)
The last formula says that if A is universally valid, A generates a rule to be logically followed. A special case of Eq. (29.4) (it is justified by the deduction theorem) is captured by
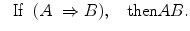
(29.5)