Optimization and Resilience in Natural Resources Management
is produced with action a when the system is in state x. The expression for utility can take many forms. Examples include a function of system state 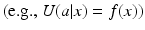 , a product of the state and action
, a product of the state and action 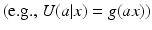 , or a measure of deviation from a critical state value
, or a measure of deviation from a critical state value ![$$(\text{e}\text{.g}\text{., }U(a|x)=r(a)h{{[x-{{x}_{0}}]}^{2}})$$](/wp-content/uploads/2015/10/A332285_1_En_12_Chapter_IEq4.gif) . In particular, the utility function
. In particular, the utility function 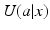 can readily incorporate system stability domains and thresholds that are the focus of ecological resilience. Note that this framework can readily absorb multi-criteria decision making by allowing the utility function to be a single expression of weighted outcomes across multiple objectives.
can readily incorporate system stability domains and thresholds that are the focus of ecological resilience. Note that this framework can readily absorb multi-criteria decision making by allowing the utility function to be a single expression of weighted outcomes across multiple objectives.
Known Process, Observable State
If x is fully observable and the utility model is known with certainty, the value function 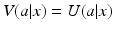 can be used to compare and contrast actions and guide decision making. The identification of an optimal action is a simple matter of comparison among options: Choose a to maximize
can be used to compare and contrast actions and guide decision making. The identification of an optimal action is a simple matter of comparison among options: Choose a to maximize 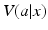 . Because the number of options is finite, this amounts to no more than selecting the largest utility from a finite list of action-specific utilities. Since the state space is finite, optimal actions can be identified for all states in finite time.
. Because the number of options is finite, this amounts to no more than selecting the largest utility from a finite list of action-specific utilities. Since the state space is finite, optimal actions can be identified for all states in finite time.
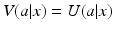 can be used to compare and contrast actions and guide decision making. The identification of an optimal action is a simple matter of comparison among options: Choose a to maximize
can be used to compare and contrast actions and guide decision making. The identification of an optimal action is a simple matter of comparison among options: Choose a to maximize 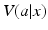 . Because the number of options is finite, this amounts to no more than selecting the largest utility from a finite list of action-specific utilities. Since the state space is finite, optimal actions can be identified for all states in finite time.
. Because the number of options is finite, this amounts to no more than selecting the largest utility from a finite list of action-specific utilities. Since the state space is finite, optimal actions can be identified for all states in finite time.Information requirements for this problem are not extensive, but nevertheless can be problematic. One must be able to specify the utility function 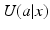 , since it is on the basis of utilities that actions are to be compared and prioritized. In addition, one must be able to identify a set of feasible and acceptable alternative actions, and provide an accurate determination of system state. Each of these requirements can pose a serious challenge to decision making. The identification of system processes and states can be especially challenging for ecosystem management , given that ecological systems are almost never fully understood and observed (see below).
, since it is on the basis of utilities that actions are to be compared and prioritized. In addition, one must be able to identify a set of feasible and acceptable alternative actions, and provide an accurate determination of system state. Each of these requirements can pose a serious challenge to decision making. The identification of system processes and states can be especially challenging for ecosystem management , given that ecological systems are almost never fully understood and observed (see below).
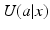 , since it is on the basis of utilities that actions are to be compared and prioritized. In addition, one must be able to identify a set of feasible and acceptable alternative actions, and provide an accurate determination of system state. Each of these requirements can pose a serious challenge to decision making. The identification of system processes and states can be especially challenging for ecosystem management , given that ecological systems are almost never fully understood and observed (see below).
, since it is on the basis of utilities that actions are to be compared and prioritized. In addition, one must be able to identify a set of feasible and acceptable alternative actions, and provide an accurate determination of system state. Each of these requirements can pose a serious challenge to decision making. The identification of system processes and states can be especially challenging for ecosystem management , given that ecological systems are almost never fully understood and observed (see below).Known Process, Unobservable State
Partially Observable State.
Often the state of a resource system is not known, but a belief state b is. Such may be the case when, e.g., probability-based monitoring of system state produces estimates of moments that can be used in constructing a distribution of state values. Under these circumstances a useful form of the value function averages utilities using the distribution probabilities b(x) for each of the possible states:
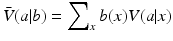
Because specification of a belief state is required for the value function, this variable appears in the expression for expected value. Assuming a known belief state b, an appropriate strategy is to maximize expected utility. The identification of an optimal action is a simple matter of comparison among options:
Choose a to maximize 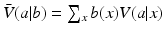
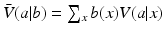
Again, this amounts to the selection of the largest value from a finite list of action-specific expected utilities. The problem, of course, is that the space of all possible belief states is a continuous simplex, so it is not possible to enumerate such a list of values for every belief state over the entire belief space. A good deal of research has been done on ways to identify optimal or near-optimal strategies over the whole belief space, under the rubric of partially observable Markov decision processes or POMDPs (see Williams 2011b).
Deeply Uncertain State.
Now assume that neither the system state nor the belief state is known. Such a situation might correspond to the lack of any observation data, or a monitoring protocol that is flawed in some unrecognizable and/or uncorrectable way. Then it no longer is meaningful to maximize an average of utilities, because there is no known distribution on which to base the averaging. A different criterion is needed to guide decision making.
One such candidate is “good enough” or robust decision making. Here the idea is not to maximize a measure of utility, but rather to produce values exceeding some specified lower limit 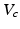 over as large a range of belief states as possible. Said differently, the intent of robust decision making is to choose an action that will maximize the range of belief states for which the expected utility for every belief state in that range will be “good enough.” This shifts the focus from maximizing expected utility to maximizing coverage of “good enough” utility. One seeks the greatest extent of system states for which a minimal performance requirement is met, by employing a two-step process: (i) for each action, a region is sought in a parameter or state space over which some minimal value is sustained, and then (ii) the action maximizing the regional coverage is selected.
over as large a range of belief states as possible. Said differently, the intent of robust decision making is to choose an action that will maximize the range of belief states for which the expected utility for every belief state in that range will be “good enough.” This shifts the focus from maximizing expected utility to maximizing coverage of “good enough” utility. One seeks the greatest extent of system states for which a minimal performance requirement is met, by employing a two-step process: (i) for each action, a region is sought in a parameter or state space over which some minimal value is sustained, and then (ii) the action maximizing the regional coverage is selected.
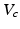 over as large a range of belief states as possible. Said differently, the intent of robust decision making is to choose an action that will maximize the range of belief states for which the expected utility for every belief state in that range will be “good enough.” This shifts the focus from maximizing expected utility to maximizing coverage of “good enough” utility. One seeks the greatest extent of system states for which a minimal performance requirement is met, by employing a two-step process: (i) for each action, a region is sought in a parameter or state space over which some minimal value is sustained, and then (ii) the action maximizing the regional coverage is selected.
over as large a range of belief states as possible. Said differently, the intent of robust decision making is to choose an action that will maximize the range of belief states for which the expected utility for every belief state in that range will be “good enough.” This shifts the focus from maximizing expected utility to maximizing coverage of “good enough” utility. One seeks the greatest extent of system states for which a minimal performance requirement is met, by employing a two-step process: (i) for each action, a region is sought in a parameter or state space over which some minimal value is sustained, and then (ii) the action maximizing the regional coverage is selected.More formally, robust decision making is defined in terms of a range of belief states, which in turn is specified for a belief state 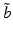 in terms of a parameter
in terms of a parameter 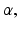 called the uncertainty horizon:
called the uncertainty horizon:
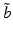 in terms of a parameter
in terms of a parameter 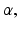 called the uncertainty horizon:
called the uncertainty horizon:![$$ R(\alpha,\tilde{b})=\left\{b:\sum\nolimits_{x}{b(x)=1\text{ and }\max [0,(1-\alpha)\tilde{b}(x) ]\le b(x)\le \min [1,(1+\alpha)\tilde{b}(x) ]\forall x\in X} \right\}. $$](/wp-content/uploads/2015/10/A332285_1_En_12_Chapter_Equb.gif)
The belief state 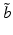 roughly plays the role of a location parameter, and
roughly plays the role of a location parameter, and 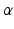 plays the role of a shape or spread parameter. The range essentially specifies a set of belief states located around
plays the role of a shape or spread parameter. The range essentially specifies a set of belief states located around 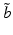 , with an extent given by
, with an extent given by 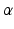 . It is clear that more belief states are included in a range corresponding to a larger uncertainty horizon
. It is clear that more belief states are included in a range corresponding to a larger uncertainty horizon 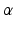 . A key question is how large
. A key question is how large 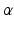 should be.
should be.
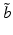 roughly plays the role of a location parameter, and
roughly plays the role of a location parameter, and 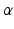 plays the role of a shape or spread parameter. The range essentially specifies a set of belief states located around
plays the role of a shape or spread parameter. The range essentially specifies a set of belief states located around 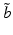 , with an extent given by
, with an extent given by 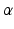 . It is clear that more belief states are included in a range corresponding to a larger uncertainty horizon
. It is clear that more belief states are included in a range corresponding to a larger uncertainty horizon 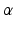 . A key question is how large
. A key question is how large 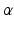 should be.
should be.Robust decision making is framed in terms of an action-specific “robustness function” that incorporates a range of belief states and a performance measure 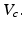 Thus, for a given action one seeks the largest uncertainty horizon
Thus, for a given action one seeks the largest uncertainty horizon 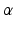 for which
for which 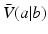 is greater than the critical value
is greater than the critical value 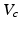 for every belief state in
for every belief state in 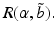 The robustness function
The robustness function 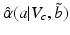 gives the uncertainty horizon identified by this maximization:
gives the uncertainty horizon identified by this maximization:
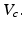 Thus, for a given action one seeks the largest uncertainty horizon
Thus, for a given action one seeks the largest uncertainty horizon 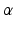 for which
for which 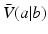 is greater than the critical value
is greater than the critical value 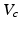 for every belief state in
for every belief state in 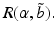 The robustness function
The robustness function 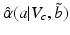 gives the uncertainty horizon identified by this maximization:
gives the uncertainty horizon identified by this maximization: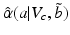
Robust decision making is then defined for a given critical value 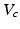 and guesstimate
and guesstimate 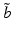 by the selection of the action with the largest uncertainty horizon given by the robustness function:
by the selection of the action with the largest uncertainty horizon given by the robustness function:
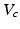 and guesstimate
and guesstimate 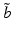 by the selection of the action with the largest uncertainty horizon given by the robustness function:
by the selection of the action with the largest uncertainty horizon given by the robustness function:Choose a to maximize 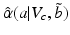 .
.
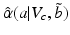 .
.The form of this maximization criterion makes it clear that robust decision making focuses on maximizing the reliability or “robustness” of expected utility, rather than the expected utility itself. The range of reliability declines as the performance requirement increases; conversely, the performance requirement must decline to obtain an expanded range of reliability. At one extreme the range of reliability shrinks to a single belief state 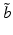 as the performance criterion converges to the optimal expected utility
as the performance criterion converges to the optimal expected utility 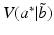 . At the other extreme, the range of reliability expands to include the entire belief space as the performance criterion shrinks to 0.
. At the other extreme, the range of reliability expands to include the entire belief space as the performance criterion shrinks to 0.
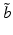 as the performance criterion converges to the optimal expected utility
as the performance criterion converges to the optimal expected utility 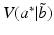 . At the other extreme, the range of reliability expands to include the entire belief space as the performance criterion shrinks to 0.
. At the other extreme, the range of reliability expands to include the entire belief space as the performance criterion shrinks to 0.Because belief space is continuous, it is not possible to conduct such an assessment for every belief state 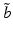 individually. One way to avoid this problem is to seek a robust decision at only one belief state
individually. One way to avoid this problem is to seek a robust decision at only one belief state 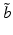 that is identified a priori. Another is to select a finite set of belief states, identify a robustness function for each, and use the results to make inferences to the remainder of the belief space.
that is identified a priori. Another is to select a finite set of belief states, identify a robustness function for each, and use the results to make inferences to the remainder of the belief space.
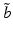 individually. One way to avoid this problem is to seek a robust decision at only one belief state
individually. One way to avoid this problem is to seek a robust decision at only one belief state 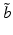 that is identified a priori. Another is to select a finite set of belief states, identify a robustness function for each, and use the results to make inferences to the remainder of the belief space.
that is identified a priori. Another is to select a finite set of belief states, identify a robustness function for each, and use the results to make inferences to the remainder of the belief space.Unknown Process, Observable State
Structurally Uncertain Process.
In a context of one-time decision making, “structural uncertainty” is expressed as a lack of certainty about the processes that lead to production of utilities. One way to represent structural uncertainty with finite-state, finite-action decision processes is to recognize variation in the utilities 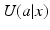 within the actions (Regan et al. 2005). Another is to assume a set of K process models that produce the utilities by
within the actions (Regan et al. 2005). Another is to assume a set of K process models that produce the utilities by 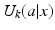 . We use the latter approach here.
. We use the latter approach here.
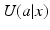 within the actions (Regan et al. 2005). Another is to assume a set of K process models that produce the utilities by
within the actions (Regan et al. 2005). Another is to assume a set of K process models that produce the utilities by 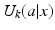 . We use the latter approach here.
. We use the latter approach here.For now, system state is assumed to be known but the process that produces utilities is not. Structural uncertainty is expressed in terms of K process models and a model state q that assigns probability q(k) to model k. The value function averages model-specific utilities 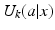 over the model state to obtain an expected value function:
over the model state to obtain an expected value function:
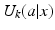 over the model state to obtain an expected value function:
over the model state to obtain an expected value function: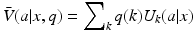
Because specification of both a system state and model state are required for the value function, both conditioning variables appear in the expression for expected value.
Assuming system observability and a known model state q, the identification of an optimal action is a simple matter of comparison among options: Choose a to maximize 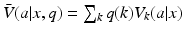 . Again, this amounts to the selection of the largest value from a finite list of action-specific expected utilities. The problem, of course, is that the space of all possible model states is a continuous simplex, so it is not possible to enumerate such a list of values for every model state over the entire model space. Williams (2011b) has shown how the approaches developed for POMDPs can be applied to the problem of structural uncertainty.
. Again, this amounts to the selection of the largest value from a finite list of action-specific expected utilities. The problem, of course, is that the space of all possible model states is a continuous simplex, so it is not possible to enumerate such a list of values for every model state over the entire model space. Williams (2011b) has shown how the approaches developed for POMDPs can be applied to the problem of structural uncertainty.
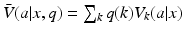 . Again, this amounts to the selection of the largest value from a finite list of action-specific expected utilities. The problem, of course, is that the space of all possible model states is a continuous simplex, so it is not possible to enumerate such a list of values for every model state over the entire model space. Williams (2011b) has shown how the approaches developed for POMDPs can be applied to the problem of structural uncertainty.
. Again, this amounts to the selection of the largest value from a finite list of action-specific expected utilities. The problem, of course, is that the space of all possible model states is a continuous simplex, so it is not possible to enumerate such a list of values for every model state over the entire model space. Williams (2011b) has shown how the approaches developed for POMDPs can be applied to the problem of structural uncertainty.Deeply Uncertain Process.
Just as it is possible with partially observable systems to shift the focus from maximizing expected utility to robust decision making, so is it possible to make such a shift with structurally uncertain systems. Assuming system state is observable but neither the appropriate model nor the likelihoods of the alternative models are known, it no longer is meaningful to maximize expected utilities over a model state. A reasonable alternative is robust decision making. In this case an uncertainty horizon and range of model states can be identified, following the same argument as above for belief states. Thus, the range of model states for an uncertainty horizon 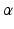 and guesstimate
and guesstimate 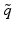 of the model state is given by
of the model state is given by
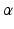 and guesstimate
and guesstimate 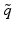 of the model state is given by
of the model state is given by![$$ R(\alpha,\tilde{q})=\left\{q:\sum\nolimits_{k}{q(k)=1\text{ and }\max [0,(1-\alpha)\tilde{q}(k) ]\le q(k)\le \min [1,(1+\alpha)\tilde{q}(k) ],k=1,\ldots{},K} \right\}. $$](/wp-content/uploads/2015/10/A332285_1_En_12_Chapter_Eque.gif)
Here one seeks the largest uncertainty horizon such that expected values for all model states in the associated range 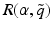 exceed a minimum value
exceed a minimum value 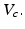 As above, this condition can be specified by
As above, this condition can be specified by
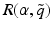 exceed a minimum value
exceed a minimum value 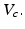 As above, this condition can be specified by
As above, this condition can be specified by![$$ \underset{\alpha }{\mathop{\max }}\,[\underset{q\in R(\alpha,\tilde{q})}{\mathop{\min }}\,\bar{V}(a|x,q)\ge {{V}_{c}}] $$](/wp-content/uploads/2015/10/A332285_1_En_12_Chapter_Equf.gif)
A robustness function 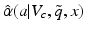 identifies the uncertainty horizon identified by this maximization. Robust decision making then consists of choosing the action that maximizes this function.
identifies the uncertainty horizon identified by this maximization. Robust decision making then consists of choosing the action that maximizes this function.
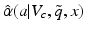 identifies the uncertainty horizon identified by this maximization. Robust decision making then consists of choosing the action that maximizes this function.
identifies the uncertainty horizon identified by this maximization. Robust decision making then consists of choosing the action that maximizes this function.Again, this form of decision making involves the replacement of a selection criterion based on maximizing expected utility with one based on maximizing the broadest possible range of minimally acceptable values of expected utility. Of course, the challenge of finding an optimal strategy over the whole model space is even greater than with partially observable systems, because a different strategy is required for every system state x.
Deeply Uncertain Process, Deeply Uncertain State
We also can consider a situation in which both forms of deep uncertainty are present. Williams (2009) discussed parameterizations and computing forms for iterative decision making with models that include structural uncertainty and partial observability . Here we consider robust decision making in the face of deep uncertainty about both factors.
In principle the approach is straightforward, in that it builds on the development above for each uncertainty factor. One can define a value function in terms of both structural uncertainty and partial observability, as
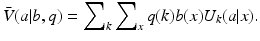
Similarly, a range of belief and model states can be defined by