Law Explorer

Fastest Law Insight Engine

In Defense of the Expressive Conception of Norms

30 Nov, 2015 GENERAL LAW







their Expressivist (hereinafter: our Expressivist) can distinguish derived obligations from explicit ones by the fact that derived obligations figure only as members of the set Cn(A), whereas the explicit obligations figure as members of both sets, the axiomatic basis A and the normative system Cn(A). Although a norm can thus belong to both these two sets, the concept of derived norms and that of explicit norms are mutually exclusive:



Def. 28.2

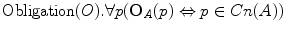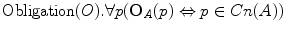$$\text{Obligation}(O ). \forall p({{\textbf{O}}_{A}}(p)\Leftrightarrow p\in Cn(A) )$$ For every p, ‘It is obligatory in A that p’ if and only if p belongs to the set Cn(A).

Def. 28.3

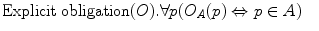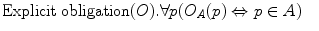$$\text{Explicit obligation}(O).\forall p({{O}_{A}}(p)\Leftrightarrow p\in A )~~~$$ For every p, ‘It is explicitly obligatory in A that p’ if and only if p belongs to the set A.

Def. 28.4

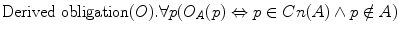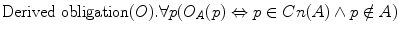$$\text{Derived obligation}(O).\forall p({{O}_{A}}(p)\Leftrightarrow p\in Cn(A)\wedge p\notin A )$$ For every p, ‘It is implicitly obligatory in A that p’ if and only if p belongs to the set Cn(A), but not to its subset A.

In the same way, our Expressivist can define the concepts of prohibition and permission for normative propositions (or states of affairs).

A proposition (or state of affairs) p is prohibited in A if and only if the negation of p (or, shortly, not-p) has been explicitly commanded or is a derived prohibition, that is a consequence of the propositions that have been commanded. To put the same in terms of sets again: “p is prohibited in A if and only if the negation of p (not-p) is a member of the [normative] system Cn(A)”,8 or of both the normative system Cn(A) and its axiomatic basis, the commanded set A.

Just as in the case of obligations, our Expressivist can thus distinguish derived prohibitions from explicit ones by the fact that derived prohibitions only figure as members of the set Cn(A), whereas explicit prohibitions figure as members of both sets, the axiomatic basis A and the normative system Cn(A):



Def. 28.5

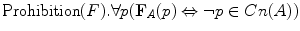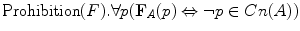$$\text{Prohibition}(F ).\forall p({{\textbf{F}}_{A}}(p )\Leftrightarrow \neg p\in Cn(A ) )$$ For every p, ‘It is prohibited in A that p’ if and only if not-p belongs to the set Cn(A).

Def. 28.6 

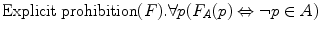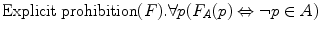$$\text{Explicit prohibition}(F). \forall p({{F}_{A}}(p )\Leftrightarrow \neg p\in A )$$ For every p, ‘It is explicitly prohibited in A that p’ if and only if not-p belongs to the set A.

Def. 28.7

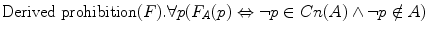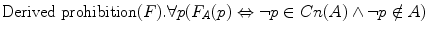$$\text{Derived prohibition}(F). \forall p({{F}_{A}}(p )\Leftrightarrow \neg p\in Cn(A )\wedge \neg p\notin A )$$ For every p, ‘It is implicitly prohibited in A that p’ if and only if not-p belongs to the set Cn(A), but not to its subset A.

A proposition (or state of affairs) p is permitted in A if and only if the negation of p (shortly, not-p) has not been explicitly commanded and is not a derived prohibition, that is a consequence of the propositions that have been commanded. In terms of sets: p is permitted in A if and only if “the negation of p (not-p) is not a member of the [normative] system Cn(A)”.9 Here is a formula:



Def. 28.8

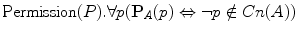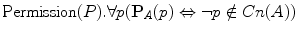$$\text{Permission}(P ).\forall p({{\textbf{P}}_{A}}(p )\Leftrightarrow \neg p\notin Cn(A ) )$$ For every p, ‘It is permitted in A that p’ if and only if not-p does not belong to the set Cn(A).

This holds for both weak or negative permissions and strong or positive permissions (inasmuch as the sufficient conditions of the former are necessary conditions of the latter). But it does not let us distinguish between the two. So, how can the Expressivist of Alchourrón and Bulygin (1981) account for the difference between them? As we will now see, the authors faced this question directly.10

Say that Rex is to permit p by saying: “I hereby allow that p!” Our Expressivist can analyse this speech act in (at least) two ways.11 She can describe this act either (a) as the act of rejection of not-p or (b) as the act of permitting p. I will call the former an Ockhamite reduction and the latter a Moritzian analysis.12 In either case, the rejected or permitted content cannot be put in the commanded set A, and this for two obvious reasons:13 (i) on the one hand, we could not distinguish permitted states of affairs from the obligatory ones and the prohibited ones if we were to put all these contents together; (ii) on the other hand, we would do nothing but introduce contradictory propositions into the normative system.

In order to avoid these problems, Alchourrón and Bulygin (1981) propose to form separate sets: the derogandum or the rejected set D in the first case, the permitted set P in the second.14

An expressivist allowing for the normative act of giving or granting permission—that is, a Moritzian expressivist—can distinguish the strongly permitted propositions or states of affairs from weakly permitted ones by the fact that only the former figure as members of the permitted set P:



Def. 28.9

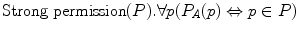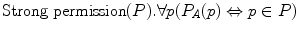$$\text{Strong permission}(P).\forall p({{P}_{A}}(p )\Leftrightarrow p\in P )$$ For every p, ‘It is strongly permitted in A that p’ if and only if p is an element of the permitted set P.

Def. 28.10

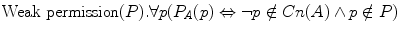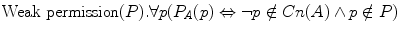$$\text{Weak permission}(P). \forall p({{P}_{A}}(p )\Leftrightarrow \neg p\notin Cn(A )\wedge p\notin P )$$ For every p, ‘It is weakly permitted in A that p’ if and only if not-p does not belong to the set Cn(A) and p does not belong to the permitted set P.

On the alternative (Ockhamite) analysis of “I hereby allow that p!”, our Expressivist can distinguish the positively permitted propositions or states of affairs from negatively permitted ones by the fact that only the negations of the former figure as members of the derogandum or the set of the explicitly rejected propositions:



Def. 28.11

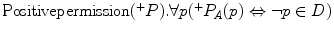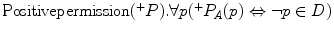$$\text{Positivepermission}({}^{+}P ). \forall p({}^{+}{{P}_{A}}(p)\Leftrightarrow \neg p\in D )$$ For every p, ‘It is positively permitted in A that p’ if and only if not-p is an element of the rejected set D.

Def. 28.12

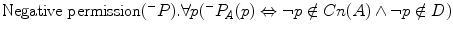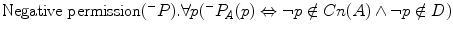$$\text{Negative permission}(^{-}P ). \forall p(^{-}{{P}_{A}}(p )\Leftrightarrow \neg p\notin Cn(A )\wedge \neg p\notin D )$$ For every p, ‘It is negatively permitted in A that p’ if and only if not-p belongs neither to the set Cn(A) nor to the rejected set D.

That having been said, one can find all of the fundamental distinctions (explicit and derived obligations, explicit and derived prohibitions, strongly and weakly permitted states of affairs) in the expressive conceptions of norms. Q.E.D.15



28.3 Facultativity Without Contradiction in the System


The fact of working with separate sets (the commanded set A on the one hand and, on the other, the permitted set P and/or the derogandum D) saves us from having contradictions in the system in case there is some facultative state of affairs. This can be demonstrated by answering the following question: What effects does an act of rejection produce on the normative system Cn(A),16 and, alternatively,17 what happens with p as a result of its being permitted?—Let us play with two examples.

First example Suppose Rex is to say “I hereby allow you to smoke!” and that p stands for  <you, smoking>. Now, we can describe this act of Rex as the act of rejection of not-p. This is an Ockhamite reduction. If not-p is not a member of the normative system Cn(A) (smoking has not been explicitly prohibited nor is the prohibition of smoking a consequence of other propositions that have been commanded), then the Cn(A) stays unchanged. However, if not-p were promulgated later, or if it were a consequence of some propositions commanded in the future, this fact would give rise to a ‘conflict of ambivalence’ between Cn(A) and D,18 which is a special case of what I would call a conflict of non-cotenability:



Def. 28.13

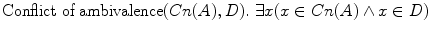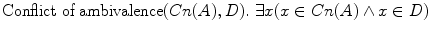$$\text{Conflict of ambivalence}(Cn(A ),D ). ~\exists x(x\in Cn(A )\wedge x\in D )$$ There is at least one x such that x belongs to the set Cn(A) and x belongs to the set D.

Def. 28.14

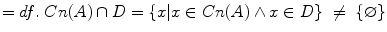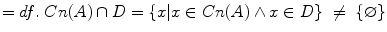$$=df.~ Cn(A )\cap D=\{x|x\in Cn(A )\wedge x\in D\}\text{ }\ne \text{ }\{\varnothing \}$$ The intersection of Cn(A) with D is not an empty set.



Def. 28.15

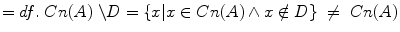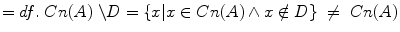$$=df.~ Cn(A )\text{ }\backslash D=\{x|x\in Cn(A )\wedge x\notin D\}\text{ }\ne \text{ }Cn(A )$$ The difference between Cn(A) and D—that is, the set of elements which belong to Cn(A) but not to D—is not equal to Cn(A).

If we want a normative system capable of guiding behavior effectively, such a conflict needs to be resolved by the application of some rule of preference,19 just as it needs to be resolved when the explicitly rejected proposition is already a member of the normative system Cn(A).

If the explicitly rejected proposition not-p is a member of the normative system Cn(A)—that is, if smoking has been prohibited either explicitly or as a consequence of other explicitly commanded propositions before Rex uttered “I hereby allow you to smoke!”—then we have a conflict of ambivalence and need some rule of preference to resolve it. If it is resolved in favor of rejection, then the proposition not-p must be eliminated by subtraction from the commanded set A and from the normative system Cn(A). This subtraction henceforth makes the (normative) proposition O A (¬p) false. If the conflict is resolved in favor of promulgation, then the proposition not-p must be subtracted from the rejected set D.

On the alternative (Moritzian) analysis of “I hereby allow you to smoke!”, we can describe this act of Rex as an act of permitting. The explicitly permitted ­proposition p is thus added to the permitted set P and another conflict of non-cotenability takes place between Cn(A) and P (it is slightly different from the one between Cn(A) and D):



Def. 28.16

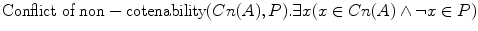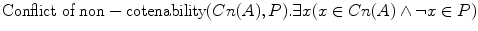$$\text{Conflict of non}-\text{cotenability}(Cn(A ),P ). \exists x(x\in Cn(A )\wedge \neg x\in P )$$ There is a least one x such that x belongs to Cn(A) and not-x belongs to P.

Def. 28.17

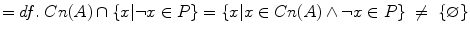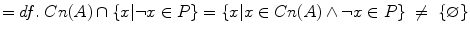$$=df.~ Cn(A )\cap \{x|\neg x\in P\}=\{x|x\in Cn(A )\wedge \neg x\in P\}\text{ }\ne \text{ }\{\varnothing \}$$ The intersection of Cn(A) with the set of negations of the elements of P is not an empty set.

Def. 28.18

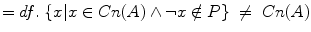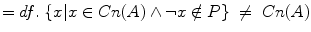$$=df.~\{x|x\in Cn(A )\wedge \neg x\notin P\}\text{ }\ne \text{ }Cn(A )$$ The set of the elements of Cn(A) the negations of which do not belong to P—is not Cn(A).

In order to resolve such a conflict, Alchourrón and Bulygin (1981) invite us to apply the rules of preference and subtract either p from the permitted set P—if the preference is given to prohibition—or the negation of p from A and Cn(A), if the preference is given to permission.20 In this respect, the permission of p gives rise to the same operation as the rejection of not-p.

Second example Suppose that Rex says also “I hereby allow you not to smoke!” To wit, there are two authoritative pronouncements: “I hereby allow you to smoke!” and “I hereby allow you not to smoke!” Following Weinberger (1985), some fear that this would bring about a contradiction in the normative system Cn(A).21 However, if we follow Alchourrón and Bulygin (1981) there is no reason for fear.

As a result of the second pronouncement of Rex, the Expressivist of Alchourrón and Bulygin (1981) will either add p to the derogandum D or not-p to the permitted set P. On the first analysis, you will now find in the derogandum D both not-p (because of the first normative act of Rex) and p (because of the second normative act of Rex); however, neither p nor not-p will be in the normative system Cn(A). On the second analysis, the permitted set P is composed of two elements: p and not-p, but again none of these two elements is part of the normative system Cn(A). In either way, the mere fact that both smoking and not smoking is permitted in the Commonwealth of Rex generates no contradiction in the normative system Cn(A) as described by our Expressivist.22 Q.E.D.

Some may, however, be of the opinion that my response does not do the trick, because we still have p and not-p in the derogated set D. Navarro and Redondo (1990a) saw that as a problem some 20 years ago. Their argument (in different words) was this:23 From p and not-p anything follows, meaning that the set of all the logical consequences of D, say Cn(D), is all-inclusive. Consequently, everything must be eliminated by subtraction from the commanded set A and the normative system Cn(A). That would leave us with empty sets A and Cn(A), which is counter-intuitive and, at any rate, highly problematic.

Indeed, the conclusion is sound but the reasoning went way too far in my opinion. The Expressivist of Alchourrón and Bulygin (1981) has no need to operate with Cn(D) as the set of all the logical consequences of D. In order to know what to eliminate from A and Cn(A), our Expressivist has to identify the “propositions and sets of propositions that imply some of the propositions belonging to [D]”.24 In other words: she needs to operate with propositions and sets of which the elements of D are a logical consequence, and not vice versa.25 The problem, therefore, does not exist.

I know that, intuitively, some will find it hard to buy the claim that there is in general no need for our Expressivist to operate with Cn(D) or Cn(P). But I am unaware of any interesting challenge, and as long as they do not provide one, only few things can be added.

One should think of two rejections, or of two permissions, that—by ways of logical inference—give rise to a third one. However, the examples of the kind usually provided by the skeptics are inadequate. (I conjecture this is because they are influenced by the Hyleticist worldview.)26 Suppose the following two rules are promulgated in the Commonwealth of Rex:



(R1)

“If φ-ing is permitted, then ψ-ing is permitted.”

(R2)

“φ-ing is permitted.”

These two rules do give rise to:



(R3)

ψ-ing is permitted.

But—unlike the Hyleticist—our Expressivist would analyze R1 as a command, and not as a permission. The propositional content of R1 (which is yet to be precised, but for the present purposes pretend it were: if p, then q) will, therefore, appear in the axiomatic basis A.27 The propositional content of R2 (that is, p) will appear in the permitted set P (or, in the Ockhamite alternative, its negation will appear in the derogandum D). The introduction of q in P (or the introduction of not-q in D) is thus not a logical consequence of two elements of P (or two elements of D); it is a logical consequence of an element of A and an element of P (or D). This example therefore cannot show the need to operate with Cn(P) or Cn(D) in order to explain the introduction of q in P (or that of not-q in D).

It is important to stress at this point that the introduction of a propositional content to a set, or its elimination thereof, is just a metaphor. If a content does not belong to a certain set, it never starts belonging to it. And if it belongs to a certain set, it never ceases to belong to it.28 What really happens is the performance of a normative speech act (commanding, rejecting; permitting if you will), which is an empirical fact. Each time a new fact occurs, we get new descriptions of the world in terms of sets. Thus in the course of time we have not one, but a sequence of sets (A 1, A 2, … A n; Cn(A 1), Cn(A 2), … Cn(A n); D 1, D 2, … D n; P 1, P 2, … P n). Following this proposal of Alchourrón and Bulygin (1981), a consecutive set A, D or P may always be defined in relation with the previous set of the same sort and the propositional content which is the object of the newly occurred speech act. If we use the signs ‘!’, ‘¡’ and ‘*’ to indicate the kind of normative speech act performed (command, rejection or permission), and ‘p’ for its propositional content, then we can represent as follows three (additional) axioms of the expressivist theory, which have not been explicitly formulated by the authors:



Axiom 1 

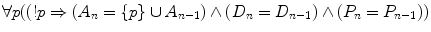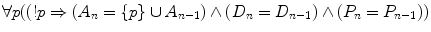$$\forall p((!p\Rightarrow ({{A}_{n}}=\left\{p \right\}\cup {{A}_{n-1}})\wedge ({{D}_{n}}={{D}_{n-1}})\wedge ({{P}_{n}}={{P}_{n-1}}))$$ For every p, if p has just been commanded, then the new set A n consists of p and all the elements of the previous set A n-1, whereas the new sets D n and P n equal the previous sets D n-1 and P n-1, respectively.

Axiom 2 

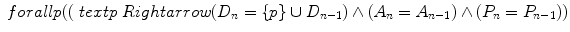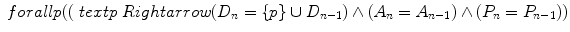$$\ forall p((\ text{}p\ Rightarrow ({{D}_{n}}=\left\{p \right\}\cup {{D}_{n-1}})\wedge ({{A}_{n}}={{A}_{n-1}})\wedge ({{P}_{n}}={{P}_{n-1}}))$$ For every p, if p has just been rejected, then the new set D n consists of p and all the elements of the previous set D n-1, whereas the new sets A n and P n equal the previous sets A n-1 and P n-1, respectively.

Axiom 3

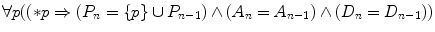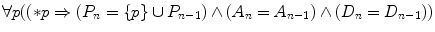$$\forall p((*p\Rightarrow ({{P}_{n}}=\left\{p \right\}\cup {{P}_{n-1}})\wedge ({{A}_{n}}={{A}_{n-1}})\wedge ({{D}_{n}}={{D}_{n-1}}))$$ For every p, if p has just been permitted, then the new set P n consists of p and all the elements of the previous set P n-1, whereas the new sets A n and D n equal the previous sets A n-1 and D n-1, respectively.

The normative system Cn(A n), on the other hand, is just the set of all the logical consequences of A n—exactly as it was explicitly defined by Alchourrón and Bulygin.29


28.4 The Propositional Content of Rules About Rules

Only gold members can continue reading. Log In or Register to continue